Initial Publication Date: August 10, 2007

Clapeyron Equation

Andrea Koziol (University of Dayton) and Dexter Perkins (University of North Dakota)

The Clapeyron equation (also called the Clausius-Clapeyron equation) relates the slope of a reaction line on a phase diagram to fundamental thermodynamic properties.

What is the Clapeyron Equation?


The reaction brucite = periclase + H2O. This reaction has a typical shape for a dehydration (or decarbonation reaction). Figure from D. Perkins.
AbJdQz
The reaction jadeite + quartz = albite. This reaction is responsible for producing jadeite in high P/T (blueschist) metamoprhic rocks. Figure from D. Perkins.


The form of the Clapeyron equation most often used is

  • dP/dT = ΔS/ΔV

This equations states that the slope (rise/run) of an univariant equilibrium plotted on a P-T diagram is equal to the entropy change (ΔS) of the reaction divided by the volume change (ΔV) of the reaction.

Using the Clapeyron equation, only the slope of the equilibrium is determined, not the actual position of the reaction in pressure-temperature space. The position must be determined by further thermodynamic calculations or by experiments.

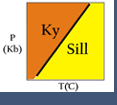
Consider the two figures above. For solid-solid reactions, such as kyanite = sillimanite or albite = jadeite + quartz, the ratio ΔS/ΔV is constant or nearly so, and so the equilibrium plots as a straight line in P-T space. For reactions involving a gas or fluid phase (such as H2O and/or CO2), the ratio ΔS/ΔV varies with P and T. This is because of increasing entropy as a gas is produced, and the extreme compressibility of the fluid. This is why reactions involving a fluid such as brucite = periclase + H2O are curved.

Potential Applications

The Clapeyron equation has many potential uses. Some examples are:
  • We can determine the slope of a metamorphic reaction from thermodynamic data to determine if it could be a potential geothermometer or geobarometer. A reaction with a shallow dP/dT slope is more sensitive to pressure changes and could be a geobarometer. A reaction with a steep (nearly vertical) slope is sensitive to temperature and could be a geothermometer.
  • If we have experimental results on some reaction at 1 temperature (or pressure), we can calculate the slope and extrapolate to other conditions instead of doing more time-consuming experiments.
  • The Clapeyron equation helps us determine thermodynamic values for reactions or phases. When combined with volume data, we can use the slope of an experimentally-determined reaction to calculate the Δ S of the reaction, and to calculate the entropy of formation (ΔSf) of a particular phase. Often the volumes of phases are very well-known, but the entropy data may have large uncertainties.
  • If we perform a Schreinemakers analysis of an invariant point, we can use the Clapeyron equation to position reactions correctly about the point.

Worked Example

Click here (Acrobat (PDF) 84kB Jun20 07) to obtain a pdf version of this example.
Problem -- Consider the reaction between grossular, corundum, anorthite and gehlenite:
Gr + Co = An + Ge

Boettcher (1970, J. Petrology 11, 337-79) determined that this reaction takes place between 760 and 780 °C at 1 Kbar pressure. Use Boettcher's results as a starting point and apply the Clausius-Clapeyron Equation to determine the temperature of reaction at 10 Kbar.

Answer -- This is a solid-solid reaction, so it is reasonable to assume that ΔS/ΔV of reaction is about constant. So we can calculate the slope of the reaction at 1bar and use that to extrapolate.

Reacton involving Gr-Co-An-Ge
The reaction Gr+Co=An+Ge, extrapolated from Boettcher's (1970) experimental results (open and closed circles) to 10 Kbar. Figure from D. Perkins.
From thermodynamic reference books, we find the following 1-bar molar entropy and volume values for the four phases involved:
  • The molar entropies of Gr, Co, An, and Ge are 255.5, 50.92, 199.3, and 209.8 J/deg, respectively
  • The molar volumes of Gr, Co, An, and Ge are 125.3, 25.575, 100.79, and 90.24 Cm3, respectively
So, for this reaction:
  • ΔV = VAn + VGe - VGr - VCo = 100.79 + 90.24 - 125.3 - 25.575 = 40.155 cm3/mol
  • ΔS = SAn + SGe - SGr - SCo = 199.3 + 209.8 - 255.5 - 50.92 = 102.68 J/deg-mol
Recall the conversion factor: 10 cm3 = 1 J/bar. Now, we can use the Clapeyron equation to get:

dP/dT = ΔS/ΔV = 10*102.68/40.155 = 25.57 bar/deg

Using this value, we find that if the reaction takes place at 770 °C at 1 Kbar, it must take place at 1121 °C at 10 Kbar.

On-line Resources