P-T-t Paths

Donna Whitney, University of Minnesota

What is a P-T-t path?

Metamorphism is a dynamic process, involving changes in temperature ± pressure through time. The pressure (P) - temperature (T) - time (t) path of a metamorphic rock is the set of all P-T conditions experienced by a rock during its metamorphic history (Figure 1).

The trajectory and shape of the P-T path, the rates of metamorphic processes, and the duration of metamorphism are a function of the source of heat and the mechanisms of burial and unroofing (if pressure change is involved). Therefore, the shape of the path, combined with time information, provides information about the driving forces of metamorphism.

In many cases, P-T information may be known, but not t (time) information. The next few sections involve discussion of aspects of P-T path trajectories without specific reference to time variables (e.g. rate, duration).

What are some common P-T paths?

P-T paths are commonly described as 'clockwise' or 'anticlockwise' (a.k.a. 'counterclockwise') (Figure 2a). It is important to note that these descriptions specifically refer to the shapes of paths drawn on a diagram with a horizontal temperature axis (temperature increasing from left to right) and a vertical pressure axis (pressure increasing from bottom to top). 

Paths can be clockwise or anticlockwise, and can also vary in terms of (1) how different the prograde and retrograde segments of the path are -- very similar or very different (Figure 2b), and (2) how different the maximum pressure and maximum temperature are from each other (Figure 2c). 

How are P-T paths determined?

For some rocks, the only part of the P-T path recorded in the mineral assemblage and texture of the rock is the 'peak' of metamorphism -- the conditions of the thermal maximum (i.e., the maximum temperature and the pressure at the maximum temperature). If the rock had a sedimentary or volcanic protolith, you can infer that the rock started at the surface, reached peak conditions at some temperature and depth in the Earth, and returned to the surface (where the rock was collected). At the peak of metamorphism, the mineral assemblage presumably equilibrated, and no (or little) further reaction took place as the rock cooled and decompressed en route to the Earth's surface.

Some rocks may record more of their P-T paths. If a rock contains a partial record of its P-T path, this is both good and bad. This is good because we want as much P-T path information as possible, so as to be able to interpret the thermal/tectonic processes and history as well as possible. This is bad because the mineralogical and textural evidence for P-T path segments other than the conditions of the peak of metamorphism represent disequilibrium. In most cases, however, the evidence for disequilibrium can be very useful because it can be used to reconstruct P-T path segments.

A few common methods for inferring P-T path segments are:

1. Mineral inclusions
2. Element zoning
3. Reaction textures

How are P-T-t paths interpreted?

An important part of using P-T paths or P-T-t paths to understand metamorphic and tectonic processes is to relate the P-T conditions, path shape, and (if age information is available) duration and rate of P-T path segments to the driving forces of metamorphism.

P-T path shape by itself does not provide a unique interpretation of tectonic process or metamorphic driving forces. For example, clockwise paths can form in continental collision belts of subduction zones. Similarly, some subduction zone rocks record clockwise paths and some record counterclockwise paths. However, the integration of P-T path characteristics, time/rate information, structural data, and other petrologic information can provide significant information about metamorphic and tectonic processes. Therefore, although subduction zone rocks can follow various paths during subduction and exhumation, determining the specific path that a particular exhumed subduction zone rock followed is important for understanding subduction dynamics.

Integrating deformation into P-T-t histories: P-T-t-d paths

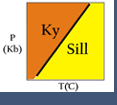
The idealized view of P-T paths is that mineral assemblages equilibrate at every stage of the path from the onset of metamorphism to the peak of metamorphism, at which the final assemblage is locked in. This view ignores kinetic factors related to the energetics of nucleation and growth of minerals, although these factors may be important for some metamorphic phases and reactions. For example, the presence of coexisting andalusite and sillimanite (Fig. 6a) in a rock that equilibrated at P-T conditions corresponding to the stability field of sillimanite illustrates that the sluggish kinetics of the andalusite-to-sillimanite transformation allowed andalusite to persist metastably outside its stability field.

It is important to recognize the influence of deformation on metamorphic reactions, and the extent to which deformation (strain energy) may assist reactions. It is possible that two rocks of the same bulk composition that follow the same P-T path but that have different deformation histories (e.g., one is pervasively deformed and the other is not, perhaps because strain is localized in weaker rocks nearby) will contain different mineral assemblages. The deformed rock may contain the predicted equilibrium assemblage for the P-T conditions attained by the rock, whereas the undeformed or less deformed rock may contain more metastable phases. P-T conditions and paths should therefore be considered in their structural context, and, if possible, a P-T-t-d path (Pressure-Temperature-time-deformation) constructed.

Deriving Geothermal Gradients

Dmitry Dolivo-Dobrovolsky has provided a computer program for deriving continental geotherms. PT_Gtrm: the program for fitting continental conductive geotherms to clouds of PT points according to approximated models of H.N. Pollack & D.S. Chapman (1977) and D. Hasterok D. & D.S. Chapman (2011). PT_Gtrm is a freeware program for fitting continental conductive geotherms to clouds of PT points, e.g. to results of geothermobarometric investigations of mantle xenoliths. This program is not intended for simulations of temperature changes with depth: it uses simple but enough precise approximating expressions with physically meaningless coefficients.PT_Gtrm approximates two models of continental conductive geotherms:

1. Pollack H.N. & Chapman D.S. On the regional variations of heat flow, geotherms and lithosphere thickness // Tectonophysics, 1977, v.38, n.3-4, p.279-296 DOI:10.1016/0040-1951(77)90215-3(link is external)
   Chapman D.S. & Pollack H.N. Regional geotherms and lithospheric thickness // Geology, 1977, v.5, n.5, p.265-268 DOI:10.1130/0091-7613(1977)5<265:RGALT>2.0.CO;2(link is external)
2. Hasterok D. & Chapman D.S. Heat production and geotherms for the continental lithosphere // Earth Planet. Sci. Lett., 2011, v.307, n.1-2, p.59–70 DOI:10.1016/j.epsl.2011.04.034(link is external)

Examples

• Metapelites Lab (Acrobat (PDF) 160kB Mar29 07) - This one week exercise, provided by Dave Pattison at the University of Calgary, includes problems sets involving petrogenetic grids, AFM diagrams, bulk compositions, mineral assemblages and isograds, as well as the use of program Gibbs.
• Phase Diagram Projections and Phase Diagram Sections Lab (Microsoft Word 40kB Mar29 07) - This two week exercise, provided by Dave Pattison at the University of Calgary, includes problems sets involving phase diagram sections using Gibbs (for demonstration of principles) and Perple_X.