Initial Publication Date: August 10, 2007
Gibbs Free Energy and Other Thermodynamic Functions
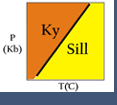
 Comparing the Gibbs Free Energy of two minerals, α and β, both with the same composition. The mineral with the lowest Energy is stable. Here we see that α is stable under some P-T conditions, and β is stable under different conditions. This image is from Bradley Hacker's lecture notes at http://www.geol.ucsb.edu/faculty/hacker/geo124T/lecture.html
Comparing the Gibbs Free Energy of two minerals, α and β, both with the same composition. The mineral with the lowest Energy is stable. Here we see that α is stable under some P-T conditions, and β is stable under different conditions. This image is from Bradley Hacker's lecture notes at http://www.geol.ucsb.edu/faculty/hacker/geo124T/lecture.html Gibbs Free Energies of Phases
All phases, whether mineralogical or not, have an associated Gibbs Free Energy of Formation value abbreviated ΔGf. The ΔGf value describes the amount of energy that is released or consumed when a phase is created from other phases.Consider, for example, enstatite (MgSiO3). The Gibbs Free Energy of Formation for enstatite from pure elements (Mg, Si and O) = ΔGf (enstatite, elements) is about -1,460.9 J/mole at room temperature and pressure. The Gibbs Free Energy of Formation for enstatite from oxides (MgO and SiO2) = ΔGf(enstatite, oxides) is about -35.4 J/mole at room temperature and pressure. Gibbs Energy values are, most often today, given in units of joules/mole or (less commonly) calories/mole.
The ΔGf values given above for enstatite are both negative. This means that enstatite is more stable than, and will form from, the separate elements or separate oxides. Some of the energy produced will be given off as heat; some will contribute to entropy.
Gibbs Free Energies are Relative Values
Gibbs free energies are relative values, not absolute values. They allow us to compare energies of different phases but individual values by themselves have no significance. Because Gibbs Energy values are relative, we can arbitrarily assume some values in order to calculate others. So, by convention the ΔGf for any pure element is assumed to be as zero.The Gibbs Free Energy of Reaction
We can calculate the Gibbs Free energy of any reaction by summing the energies of the right-hand side of the reaction and subtracting the energies of the left hand side. For example, we can write a reaction describing the formation of enstatite from separate elements:Mg + Si + 3O = MgSiO3 (rxn 1)
The ΔG for reaction (1) is the Gibbs Free Energy of formation of enstatite from the elements (-1,460.9 J/mole at room temperature and pressure):
ΔG1 = ΔGf(enstatite, elements) = ΔGf(enstatite) - ΔGf(Mg)-ΔGf(Si)-3ΔGf(O) (Eqn 1)
All reactions have an associated ΔGrxn value but the values vary with pressure and temperature (T). If we wish to make thermodynamic calculations involving ΔGf, we must either look the values up in a book for the P-T conditions of interest, or calculate the values using standard equations.
Click here to learn more about Thermodynamic Calculations . . .
Determining the Location of Metamorphic Reactions
Consider the reaction: albite = jadeite + quartz (rxn 2)For this reaction:
ΔG2 = ΔGf (jadeite, elements) + ΔGf (quartz, elements) - ΔGf (albite, elements) (Eqn 2)
or
ΔG2 = ΔGf (jadeite, oxides) + ΔGf (quartz, oxides) - ΔGf (albite, oxides) (Eqn 3)
These two values will always come out to be the same, but most reference books list values relative to the elements. If we look up ΔGf values in a reference book, we will find that:
At 400° C and 1.0 GPa: ΔG2 > 0
At 400° C and 1.4 GPa: ΔG2 < 0
So, at 400° C and 1.0 GPa, albite is the stable form, but at 1.4GPa albite will react to form jadeite + quartz. At about 400°C and 1.18 GPa, on the reaction line, ΔG2 = 0.
For any reaction under a given set of P-T conditions: If the ΔGrxn < 0, the reaction proceeds to the right. If the ΔGrxn >0, the reaction proceeds to the left. The univariant reaction curve that separates the two assemblages actually represents the locus of points where ΔGrxn = 0
Internal Energy (E), Enthalpy (H), Entropy (S), Volume (V) of Phases and Reactions
The Gibbs Free Energy of any phase varies with pressure and temperature. The fundamental relationship is:G = E + PV - TS (Eqn 2)
or
G = H - TS (Eqn 3)
In the above expressions, P and T refer to pressure and temperature. E, V, H and S refer to the internal energy, volume, enthalpy and entropy of the phase. It follows that:
H = E + PV (eqn 4)
Similarly, for any reaction, the Gibbs Free Energy of reaction varies with pressure and temperature:
ΔGrxn = ΔErxn + PΔVrxn -TΔSrxn (Eqn 5)
or
ΔGrxn = ΔHrxn -TΔSrxn (Eqn 6)
As above, P and T refer to pressure and temperature ΔG is the Gibbs energy of reaction, ΔE is the internal energy of reaction, ΔV is the volume of reaction, ΔH is the enthalpy of reaction and ΔS is the entropy or reaction.
Look closely at Equation (5). The right hand side contains three terms. The first is the change in internal energy -- a constant depending on the phases involved. The second is a PV term -- it equates Gibbs Energy with volume and pressure. More voluminous phases have greater Gibbs Free Energy. (Recall that the energy of an ideal gas = PV = nRT.) The third term involves entropy (S). Entropy is a measure of disorder. Some phases can absorb energy simply by becoming disordered. Temperature may not increase, volume may remain the same, but energy disappears.
Chemical systems seek to minimize energy and, consequently, phases of greater Gibbs Free Energy are unstable with regard to phases with lower Gibbs Free Energy. So, at high temperature, phases with high entropy are very stable. This is because the TS term in Equation (5) has a negative sign. Similarly, at high pressure, phases with high volume are unstable. The PV term has a positive sign. (Although your intuition may not work well when considering entropy, it should seem reasonable that low volume, very dense, phases are more stable at high pressure than phases of less density.)
Intensive and Extensive Variables, and Units
P and T are termed intensive variables. G, E, H, V and S are extensive variables. The difference is that intensive variables (P and T) do NOT depend on the size of the system or the amount of material present. G, E, H, V and S do depend on system size (e.g., the larger the system, the larger the volume).Pressure is typically given in units of pascals (Pa), Gigapascals (GPa), bars (bar) or Kilobars (Kbar). G, E, and H are typically given in units of J/mole. V is in cm3/mole, and entropy in J/deg-mole. (Calories may be substituted for Joules, 1 cal = 4.186 J). Note: The PV term in the above expressions is not in the same units as the other terms. A necessary conversion factor is 1 J = 10 cc-bar.
What is the significance of the different thermodynamic variables?
- The Gibbs free energy (ΔGrxn) tells us whether a reaction will take place. ΔGrxn is the Gibbs Free Energy of the right hand side of a reaction, minus the Gibbs Free Energy of the left hand side. If ΔGrxn < 0, the reaction will proceed to the right; if it is > 0, the reaction will proceed to the left.
- The enthalpy of reaction (ΔHrxn) tells us how much heat will flow in or out of the system. If ΔHrxn < 0, the reaction is exothermic -- it releases heat. For example, combustion of carbon based compounds (C + O2 = CO2) gives off a lot of heat. If ΔHrxn > 0, the reaction is endothermic -- it consumes heat. Melting ice [H2O (ice) = H2O (water)] is endothermic and, consequently, cools our gin and tonics in the summer.
- The entropy of a reaction (ΔSrxn) tells us whether the products or reactants are more disordered. For example, the reaction of liquid water to steam (boiling) has a large associated entropy. The steam molecules are more dispersed, are less well bonded together, and have greater kinetic energy.
- The volume of a reaction (ΔVrxn) tells us whether the products or the reactants have greater volume. The reaction of graphite to diamond, both made entirely of carbon, proceeds at high pressure because diamond is more dense (has smaller volume) than graphite.
Making thermodynamic calculations
The important thermodynamic variables (G, E, H, V and S) vary with pressure (P), temperature (T) and composition (X). The relationships are not simple, and evaluating the various functions requires integral calculus. Although, in principle, it is possible to do thermodynamic calculations by hand, today most practitioners rely on computer programs.Click here to learn more about Thermodynamic Calculations . . .