Initial Publication Date: August 10, 2007
Fundamental Thermodynamic Calculations
The basis for calculating a reaction curve (a curve/line on a phase diagram) is the understanding that the Gibbs Free Energy of a reaction (ΔGrxn) can be calculated for any P-T-X conditions, provided a starting point and the requisite thermodynamic data are available. The fundamental relationship is: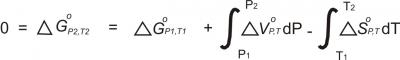
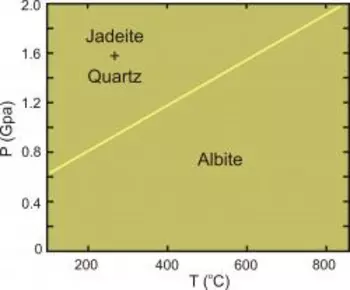Phase diagram showing the reaction :albite = jadeite + quartz. The curve can be calculated from a starting point at, for example, 800 degrees and 2 GPa, and extrapolated to higher temperaures. Along the reaction line, ΔGrxn = 0. Above the line ΔGrxn < 0; below the line ΔGrxn > 0.
ΔG, ΔV, and ΔS refer to the Gibbs Energy, volume and entropy of reaction. The degree superscript reminds us that these values are for pure phases. The P and T subscripts remind us that the values change with pressure and temperature.
The starting Gibbs Free Energy value, ΔGP1,T1, may be directly obtained from calorimetric studies. Alternatively, and more commonly, experimental studies may provide a reference point at which a particular reaction is in equilibrium (ΔGP,T = 0). In either case, the equation above is solved to find the location of the reaction curve, points at which ΔGrxn = 0. The result is a curve (often nearly a straight line) in P-T-X space that separates fields of stability for different minerals or mineral assemblages.
For reactions involving pure, end member minerals, the above equation suffices. However, many minerals are solid solutions, so the effective activity (reactivity) of mineral components is diluted. The basic thermodynamic equation is modified to take this into account by adding a term involving the equilibrium constant(K):
The equilibrium constant for a reaction (K) is the product of the activities of the reaction products, divided by the product of the activities of the reactants:
Putting It All Together: An Example
For an example, let's combine the above equations, and consider the reaction:3 anorthite = grossular + 2 kyanite + quartz
For this reaction, the conditions for thermodynamic equilibrium are:
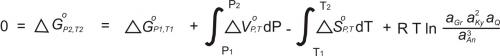
The exponents on the activity terms for kyanite and anorthite are because the reaction involves 3 moles of anorthite and 2 moles of kyanite.
If a mineral assemblage contains kyanite and quartz, they are generally nearly pure, so their activities = 1. The above equation then becomes:
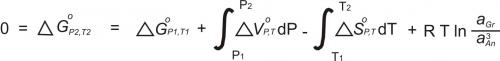
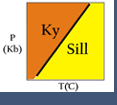
This equation is the basis for the GASP geobarometer used by some petrologists to calculate metamorphic pressures (see figure).
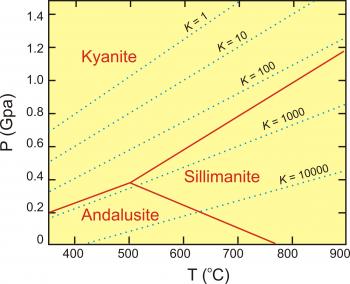Phase diagram showing values of the equilibrium constant, K for the GASP reaction 3An = Gr + Ky + 2Q. Given the compositions of coexisting minerals, K, can be calculated and, if metamorphic temperature is know, the metamorphic pressure may be read from this diagram. Also shown are the stability fields for andalusite, kyanite, and sillimanite. Depending on pressure and temperature, the GASP barometer may involve andalusite or sillimanite instead of kyanite. Calculating Activities
Some minerals, like quartz, are so pure that, when present, their activities are 1. Other minerals are more variable in composition. Consequently, the activity of a given component may vary, depending on composition. So, we use activity models to calculate the activities of the components we care about, so that we may put the values into the equations above. Activity models vary from being quite simple to very complex and may require computer programs to be useful.More information about activity models . . .
The Slope of a Reaction Curve
Sometimes, petrologists have a starting point, perhaps from experimental studies, and only need to know the slope of a reaction in order to plot it on a phase diagram. Differentiation of the equations above reveals that the slope may be calculated:dP/dT = ΔSP,T/ΔVP,T
This relationship is called the Clausius-Clapeyron equation.
More information about the Clausius-Clapeyron equation . . .