Author Profile
Initial Publication Date: August 10, 2007

Deriving and Balancing Metamorphic Reactions

Dexter Perkins (University of North Dakota)

A four page summary (Acrobat (PDF) 33kB Jul31 07) is available which can be used as a class handout.
Given a list of minerals, how do we determine all the possible reactions that can occur between them? There are many ways to approach this question and the answer can sometimes be quite elusive.

One Way To Proceed

  • Make a list of all the phases and their formulas.
  • Identify the chemical system and the number of components
  • Use the phase rule to determine how many phases are in a normal univariant reaction
  • Make a list of all possible reactions, identifying them by the phases they DO NOT contain
  • Balance the reactions

Example Involving 5 Phases and 3 Components

Consider the phases:
  • Wo: Wollastonite CaSiO3
  • Ky: Kyanite Al2SiO5
  • An: Anorthite CaAl2Si2O8
  • Gr: Grossular Ca3Al2Si3O12
  • Qz: Quartz SiO2

 The chemical system is CaO-Al2O3-SiO2; it contains 3 components. The phase rule tells us that a univariant reaction will include 4 phases (unless it is degenerate). So, each reaction will be missing one phase.

Possible reactions are (absent phase in parentheses):
  1. (Wo) involves Ky, An, Gr, Qz
  2. (Ky) involves Wo, An, Gr, Qz
  3. (An) involves Wo, Ky, Gr, Qz
  4. (Gr) involves Wo, Ky, An, Qz
  5. (Qz) involves Wo, Ky, An, Gr
Consider the first reaction (Wo). It involves kyanite, anorthite, grossular and quartz.

Inspection Method:

For fairly simple systems involving few phases, we can usually identify and balance reactions by inspection.

For this example, note that only two of the phases (An, Gr) contain Ca, so they must be on opposite sides of the reaction. Also, Gr contains 3 Ca, compared to 1 in An. Therefore we can start with:
something + 3 An = something + Gr
something + 3 CaAl2Si2O8 = something + Ca3Al2Si3O12

If we next consider balancing Al, it becomes apparent that we must put 2 Ky on the right hand side:
something + 3 An = something + Gr + 2 Ky
something + 3 CaAl2Si2O8 = something + Ca3Al2Si3O12 + 2 Al2SiO5

Finally, to balance Si, we must add 1 Qz to the right hand side:
3An = Gr + 2 Ky + 1 Qz
3 CaAl2Si2O8 = Ca3Al2Si3O12 + 2 Al2SiO5 + SiO2

Two types of reactions
Ternary diamgram: CaO-Al2O3-SiO2

Graphical Method:

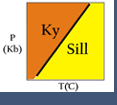
An alternative to the "inspection" method is to plot compositions on a triangular diagram.

This approach works for 3 component systems and for a 4-component system IF one of the components has the same composition as one of the phases.

If we look at the triangular diagram shown here, we can "pick off" the reactions by noting where phases plot and identifying reactions as either being tie line flip reactions or terminal reactions. In this case we see that:
  1. (Wo) is a terminal reaction: An= Gr + Ky + Q
  2. (Ky) is a tie-line flip reaction: Gr+Q=An+Wo
  3. (An) is a tie-line flip reaction: Gr+Q=Ky+Wo
  4. (Gr) is a degenerate reaction and is the same as (Qz): An = Wo + Ky
Now that we know what sides of the reaction the phases are on, balancing them becomes much simpler (although sometimes remaining difficult). For many purposes, including doing a Schreinemakers analysis, balancing reactions is not necessary as long as the phases are on the correct sides.

More Complicated Systems and More Phases

The above example (3-component system and 5 phases) is fairly straightforward. If we were to consider more phases or more components, we would soon get bogged down. For example, if we look at the same system as in the above example (CaO-Al2O3-SiO2) but add one more phase, and so consider Wo, Ky, An, Gr, Q, and Ge (gehlenite), each reaction is missing 2 phases instead of 1. There are 15 potential reactions, but one is degenerate, so we have:
  1. (Wo)(An) is a tie-line flip reaction: Gr+Ky=Ge+Qz
  2. (Wo)(Gr) is a terminal reaction: An=Ge+Ky+Qz
  3. (Wo)(Ky) is a tie-line flip reaction: Ge+Qz=Gr+An
  4. (Wo)(Qz) is a tie-line flip reaction: Ge+Ky=An+Ge
  5. (Wo)(Ge) is a terminal reaction: An= Gr + Ky + Q
  6. (An)(Gr) is a tie-line flip reaction: Ge+Qz=Wo+Ky
  7. (An)(Ky) is a terminal reaction: Gr=Wo+Ge+Qz
  8. (An)(Qz) is a terminal reaction: Gr=Wo+Ky+Ge
  9. (An)(Ge) is a tie-line flip reaction: Gr+Q=Ky+Wo
  10. (Gr)(Ky) is a tie-line flip reaction: Wo+An=Qz+Ge
  11. (Gr)(Ge)(Qz) is a degenerate reaction: An = Wo + Ky
  12. (Ky)(Qz) is a terminal reaction: Gr=Wo+An+Ge
  13. (Ky)(Ge) is a tie-line flip reaction: Gr+Q=An+Wo

Things can get complicated in a hurry!

Gauss-Jordan Reduction

When dealing with more than just a few components and phases, deriving all possible reactions using the approaches described above can be problematic. The Gauss-Jordan reduction method is a systematic approach that relies on matrix algebra. It is well described in Frank Spear's Metamorphic Phase Equilibria and Pressure-Temperature-Time Paths. (There are also many websites that try to explain the method, but most are difficult to understand.)

Click here for an Excel spreadsheet that performs Gauss-Jordan Reduction (v7, Oct 2016) (Excel 220kB Oct30 16)

Click here for a Quattro spreadsheet that performs Gauss-Jordan Reduction (n.b., this routine is inferior to the Excel version -- use that one if possible) ( 103kB Jul31 07)

An example will explain this method:

Problem: Determine all possible reaction that can occur between these 5 phases:
  • anorthite CaAl2Si2O8
  • grossular Ca3Al2Si3O12
  • wollastonite CaSiO3
  • kyanite Al2SiO5
  • quartz SiO2

Start by writing equations describing the phase compositions in terms of their elements:
1An + 0Gr + 0Wo + 0Ky + 0Qz = 1Ca + 2Al + 2Si + 8O
0An + 1Gr + 0Wo + 0Ky + 0Qz = 3Ca + 2Al + 3Si + 12O
0An + 0Gr + 1Wo + 0Ky + 0Qz = 1Ca + 0Al + 1Si + 3O
0An + 0Gr + 0Wo + 1Ky + 0Qz = 0Ca + 2Al + 1Si + 5O
0An + 0Gr + 0Wo + 0Ky + 1Qz = 0Ca + 0Al + 1Si + 2O

Now, subtract multiples of the first equation from the four below it to eliminate Ca (from the right hand side of all equations), leaving:
+1An + 0Gr + 0Wo + 0Ky + 0Qz = 1Ca + 2Al + 2Si + 8O
-3An + 1Gr + 0Wo + 0Ky + 0Qz = 0Ca - 4Al - 3Si - 12O
-1An + 0Gr + 1Wo + 0Ky + 0Qz = 0Ca - 2Al - 1Si - 5O
+0An + 0Gr + 0Wo + 1Ky + 0Qz = 0Ca + 2Al + 1Si + 5O
+0An + 0Gr + 0Wo + 0Ky + 1Qz = 0Ca + 0Al + 1Si + 2O

Now, subtract multiples of the second equation from the three below it to eliminate Al, leaving:
+1.00An + 0.00Gr + 0Wo + 0Ky + 0Qz = 1Ca + 2Al + 2.00Si + 8O
+0.75An - 0.25Gr + 0Wo + 0Ky + 0Qz = 0Ca + 1Al + 0.75Si + 3O
+0.50An - 0.50Gr + 1Wo + 0Ky + 0Qz = 0Ca + 0Al + 0.50Si + 1O
-1.50An + 0.50Gr + 0Wo + 1Ky + 0Qz = 0Ca + 0Al - 0.50Si - 1O
+0.00An + 0.00Gr + 0Wo + 0Ky + 1Qz = 0Ca + 0Al + 1.00Si + 2O

Continue this process, subtracting multiples of the third equation from the last two to eliminate Si. If you do it correctly, oxygen will be eliminated as well:

+1.00An + 0.00Gr + 0Wo + 0Ky + 0Qz = 1Ca + 2Al + 2.00Si + 8O
+0.75An - 0.25Gr + 0Wo + 0Ky + 0Qz = 0Ca + 1Al + 0.75Si + 3O
+1.00An - 1.00Gr + 2Wo + 0Ky + 0Qz = 0Ca + 0Al + 1.00Si + 2O
-1.00An + 0.00Gr + 1Wo + 1Ky + 0Qz = 0Ca + 0Al - 0.00Si + 0O
-1.00An + 1.00Gr - 2Wo + 0Ky + 1Qz = 0Ca + 0Al + 0.00Si + 0O

Notice that the right hand side of the last two equations now = 0. These two are, then:
-1.00An + 0.00Gr + 1Wo + 1Ky + 0Qz = 0
-1.00An + 1.00Gr - 2Wo + 0Ky + 1Qz = 0

Or, we can rewrite them in the more traditional way:
An = Wo + Ky
Gr + Qz = An + 2Wo

The first of these is a degenerate reaction, missing (Gr) and (Qz). The second is a terminal reaction missing (Ky). We can add and subtract these to come up with all four possible reactions:

An = Wo + Ky
Gr + Q = An + 2Wo
3 An = Gr + 2Ky + Q
Gr + Q = Ky + 3Wo

Click here for an Excel spreadsheet that performs Gauss-Jordan Reduction (Excel 220kB Oct30 16)

Click here for a Quattro spreadsheet that performs Gauss-Jordan Reduction ( 103kB Jul31 07)