Method of Schreinemakers -- A Geometric Approach to Constructing Phase Diagrams

Dexter Perkins, University of North Dakota and Dave Mogk, Montana State University

Examples of Invariant Points and Bundles of Reactions

Show caption for Example 1

Hide

This example of an invariant point in PT space includes reactions involving enstatite, corundum, cordierite, forsterite, and spinel. In this example, all reactions have two phases on each side, but that is not always the case. As is traditionally done, the reactions have been labeled by putting the "missing" phase(s) in parentheses at the end of the reaction curve.

Show caption for Example 2

Hide

This example of an invariant point in PT space includes reactions involving pyrophyllite, diaspore, zoisite, margarite, kyanite and H₂O. As is traditionally done, the reactions have been labeled by putting the "missing" phase(s) in parentheses at the end of the reaction curve. Note that there are two degenerate reactions at this invariant point (reactions involving only 4 phases). They are the nearly vertical (Mg)/(Zo) reaction, and the nearly horizontal (H₂O)/(Py) reaction.

Show caption for Example 3

Hide

This example of an invariant point in TX space includes reactions involving tremolite, calcite, dolomite, diopside, quartz, CO₂ and H₂O. As is traditionally done, the reactions have been labeled by putting the "missing" phase(s) in parentheses at the end of the reaction curve. Analyzing TX diagrams using the Schreinemakers approach is a bit different than analyzing a PT diagram because TX diagrams imply the presence of H₂O and CO₂. Note that the (Tr)(Cc) reaction is degenerate; it involves fewer phases than the others.

Start with the phase rule (P + F = C + 2). P, F, and C refer to the number of phases present, the degrees of freedom, and the number of system (chemical) components. An invariant point (where reactions intersect) has 0 degrees of freedom (F=0), a reaction line has 1 degree of freedom (F=1), and a divariant field between reactions has 2 degrees of freedom (F=2).

For a PT diagram, what the phase rule tells us is that:

• Invariant points occur at a fixed P and T. (You are NOT free to vary either if you wish to stay at the point.)
• Reaction lines occur over a range of P and T, but the two cannot be varied independently. (You are free to change either P or T, but once you do that, the value of the other is fixed at a particular value or you will not stay on the line.)
• Fields between reactions have two degrees of freedom. (You can vary both P and T, within limits, independently and you will still stay in the field.

Corrolaries to the phase rule are that, for an "n" component system (C = n):

• There are n+2 phases related by univariant reactions (F=1) around an invariant point (F=0).
• In the general case, there are n+2 univariant reaction curves that intersect at the invariant point; each reaction is represented by a univariant curve.
• In the general case, there are n+1 phases involved in each univariant reaction.
• There are n phases stable in each divariant field (F=2) and there are n+2 divariant fields.
• Special case:If one (or more) of the reactions are degenerate, the reaction(s) will include fewer than n+1 phases, there will be fewer than n+2 reaction curves, and fewer than n+2 divariant fields. (Degenerate reactions are those that can be described with fewer components than the overall system, see below. If degenerate reactions are involved at an invariant point, it may appear that there are too few univariant curves because two or more curves may a) be collinear on opposite sides of the invariant point and thus appear to be the same curve, or b) may be superimposed on top of each other, so a single curve may represent reactions with two or more phases absent).

• Reaction curves involving n+1 phases cannot pass through an invariant point because crossing other reaction curves means that some of the phases or assemblages become unstable. A reaction is said to be metastable in space where product or reactant minerals or assemblages are unstable. (Metastable curves are sometime plotted as dashed lines but for clarity are usually omitted from phase diagrams.)
• Another consequence of these relationships is that a given mineral assemblage is limited to an arc of ≤180^o; again, this is because the stability field of a mineral assemblage will be cut off by another reaction (see details about the Morey-Schreinemakers Rule in Zen, 1966).
• Degenerate reactions may, or may not, pass through an invariant point. Because a degenerate reaction is actually depicting 2 (or more) phase absent curves, these can be arranged in two ways: 1) "stable on stable", which means that the two reactions are superposed directly on top of each other (and thus terminate at the invariant point but with two phase absent labels on one end of the curve), or 2) "stable on metastable" which means each reaction is superposed on the metastable extension of the other, so the appearance is that the reaction curve passes direclty through the invariant point (but the ends of the curves are each labeled with a different phase absent). In Example 3, above, the (Tr)(Cc) reaction is an example of a stable on stable degenerate reaction. In Example 2, above, the nearly horizontal (H₂O)/(Py) reaction is an example of a stable on metastable degenerate reaction.

Click here to learn more about identifying possible reactions...

One Component Systems

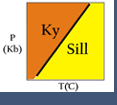
Most of the bulleted relationships (above) can be readily seen in the simple one component system (C = n = 1) Al₂SiO₅.

Show caption

Hide

The aluminosilicate phase diagram: one component (Al₂SiO₅), three univariant reactions involving three phases (andalusite, kyanite, sillimanite)

The phases andalusite, sillimanite and kyanite may coexist (n+2 phases) at an invariant point. The phases are related by 3 (n+2) univariant reaction curves, each involving 2 (n+1) phases, and these curves limit 3 (n+1) divariant fields, each of which contains either andalusite, kyanite or sillimanite (n phases).

All three univariant reactions stop at the invariant point because they become metastable beyond the point. Their extensions beyond the invariant point could have been plotted as dashed lines but it serves no useful purpose in this case.

Multicomponent Systems

Show caption

Hide

These two examples show reactions crossing, but they do not make an invariant point. In the first example (left), the two reactions take place in different chemical systems. One includes Mg, the other does not. One includes Al, the other does not. The second example involves two reactions in the CaO-Al₂O₃-SiO₂ system, but there are 6 phases between the two. The phase rule says that an invariant point for a 3 component system may only involve 5 phases. These are both examples of what are called "indifferent crossings."

In multicomponent systems, when two univariant reactions in a given system cross, they create an invariant point provided the total number of phases involved does not exceed C+2 (the number of system components + 2). If, however, the two reactions belong to different systems, or if there are too many phases between the two, the reactions may cross without creating an invariant point (see Figure, at left).

When two univariant reactions intersect at an invariant point, additional reactions also must pass through that point. Some may be stable on both sides of the point, some may be metastable on one side only, and some may be entirely metastable. The sequence of reactions around the invariant point, and their stability or metastability, depend on the compositional relationships of the phases involved.

Consider again the three examples above:

Show caption for Example 1

Hide

This example of an invariant point in PT space includes reactions involving enstatite, corundum, cordierite, forsterite, and spinel. In this example, all reactions have two phases on each side, but that is not always the case. As is traditionally done, the reactions have been labeled by putting the "missing" phase(s) in parentheses at the end of the reaction curve.

Show caption for Example 2

Hide

This example of an invariant point in PT space includes reactions involving pyrophyllite, diaspore, zoisite, margarite, kyanite and H₂O. As is traditionally done, the reactions have been labeled by putting the "missing" phase(s) in parentheses at the end of the reaction curve. Note that there are two degenerate reactions at this invariant point (reactions involving only 4 phases). They are the nearly vertical (Mg)/(Zo) reaction, and the nearly horizontal (H₂O)/(Py) reaction.

Show caption for Example 3

Hide

This example of an invariant point in TX space includes reactions involving tremolite, calcite, dolomite, diopside, quartz, CO₂ and H₂O. As is traditionally done, the reactions have been labeled by putting the "missing" phase(s) in parentheses at the end of the reaction curve. Analyzing TX diagrams using the Schreinemakers approach is a bit different than analyzing a PT diagram because TX diagrams imply the presence of H₂O and CO₂. Note that the (Tr)(Cc) reaction is degenerate; it involves fewer phases than the others.

• For each example, we could start with any two reactions. Adding and subtracting them would yield the others.
• In Example 1, the system contains 3 components (C=3: MgO-Al₂O3-SiO₂). There are 5 possible univariant reactions. Each reaction involves 4 phases (one phase is always absent). The invariant point involves 5 phases. 3 phases are stable in each divariant field.
• In Example 2, the system contains 4 components (C=4: CaO-Al₂O3-SiO₂-H₂O). Each reaction involves 5 phases, except reaction 1, which is degenerate. The invariant point involves 6 phases. 4 phases are stable in each divariant field.
• In Example 3, the system contains 5 components (C=5: CaO-MgO-SiO₂-H₂O-CO₂). This example is, however, different from the previous two because it is a T-X diagram. For a T-X diagram, pressure is held constant and the phase rule is modified to be C + 1 = P + F. However, H₂O and CO₂ are together counted as a single phase, because they mix to form one fluid. Normal univariant reactions, then, involve 5 phases. For example, the (Di) reaction involves four minerals and a fluid. Invariant points involve 6 phases, and 4 phases are stable in each divariant field. The (Tr,Cc) reaction is degenerate.
• In these three drawings the reactions have been labeled in the traditional way with the phases absent from the reaction in parentheses.

Help From Compatibility Diagrams

One useful way to make sure that reactions are arranged appropriately is to use compatibility diagrams, as shown in the large figure below.

The triangular compatibility diagrams (C=3) contain lines dividing them into triangular fields. Each triangle represents a stable mineral assemblage. Because stable assemblages change when a reaction is crossed, the tie lines change as well.

Show caption

Hide

This example shows an invariant point in the Al₂O₃-SiO₂-H₂O system involving pyrophyllite, diaspore, kaolinite, quartz and H₂O. Triangular compatibility diagrams show changes in mineral assemblages from one field to the next.

Show caption

Hide

The (Qz), (Dsp) and (Py) reactions are all stable on one side of the invariant point only. This diagram, however, shows metastable extensions of those reactions into divariant fields. Consider the (Qz) reaction: it cannot be stable up and to the left of the invariant point because the reaction involves pyrophyllite, and pyrophyllite is not stable to the left of the (Ka)(H₂0) reaction. Note that the degenerate (Ka)(H₂0) reaction passes through the invariant point. Degenerate reaction often, but not always, are stable on both sides of an invariant point.

Show caption

Hide

Two examples demonstrating the Morey-Schreinemakers Rule. The assemblage kaolinite + quartz is limited to two sectors by the reactions (Py) and (Dsp). Pyrophyllite is stable over a full 180°, only being limited by the terminal reaction (Ka)(H₂O).

• Note 1: Crossing a reaction line can either cause (a) a tie line flip (e.g. Ka + Qz = Py + H₂O) or (b) a terminal reaction, e.g. Py = Dsp + Qz). Tie-line flip reactions result in one line (on the compatibility diagram) disappearing and being replaced by a different line. Crossing a terminal reaction (a reaction that has a single phase on one side) results in a phase disappearing completely -- and involves several tie lines disappearing. (If the reaction is crossed in the other direction, a new phase and several tie lines appear).

  Click here to learn more about different kinds of reactions...

  
  
• Note 2: If a reaction is missing a particular phase (traditionally labeled by putting the absent phase in parentheses), that phase is present on the opposite side of all other reactions. For example, the (Dsp) reaction (reaction not involving diaspore) is at the bottom of the diagram, and diaspore is stable on the top side of all other reactions.
• Note 3: The metastable extension of any reaction (the dashed part of a reaction line past the invariant point) occurs in a divariant field bounded by two univariant curves that have the "absent" phase facing each other. In this diagram, for example, the (Qz) reaction extends into a field bounded by Dsp+Qz+H₂O and Dsp+Qz.
• Note 4: The Morey - Schreinemakers Rule (also called the 180° rule) says that: (a) No sector (the wedge between two reaction curves) around an invariant point can go more than 180°. (b) A divariant assemblage always occurs in a sector which makes an angle about the invariant point of ≤180°). See the figures above left, and lower right. In the diagrams shown, no single phase or phase assemblage is stable for more than 180° around the invariant point. For example, the assemblage kaolinite + quartz is limited to about 120° in the two sectors on the lower left by the reactions (Dsp) and (Py). Another example: pyrophyllite by itself enjoys a full 180° of stability (three right lower sectors).
• Note 5: As you proceed around an invariant point, within any 180° progression: 2-phase assemblages break down before either phase (in the assemblage) breaks down by itself. Similarly, a 3-phase assemblage breaks down before any 2-phase assemblage (that contains 2 of the original 3 phases), which breaks down before any of the phases by themselves. In the example above, the (Qz) reaction limits the assemblage Py-Dsp-H₂O. Proceeding clockwise, the (Dsp) reaction limits Py-H₂O. Then, the (Ka)(H₂O) reaction limits Py. Don't misinterpret this observation: it does NOT mean that the sequence 3-phase, 2-phase, 1-phase is followed for all assemblages. It just means that if 3-, 2-, and 1-phase reactions (that involve the same phases) are present, they always follow in order. For complex systems, other reactions may intervene, but the order must be followed.


Click here (Acrobat (PDF) 12kB Aug10 07) to enlarge.

Show caption

Hide

This T-X diagram shows a repeated invariant point involving the phases quartz,calcite, K-feldspar, phlogopite, diopside, and tremolite. The dashed lines are metastable parts of reaction curves. Note that the two invariant points are mirror images (enantiomorphic projections) of each other. Image from John Valley.

---

• Note 6: Because the curvature and slopes of the univariant curves may be quite variable across a phase diagram, invariant points may be duplicated. This occurs more often on T-X diagrams than on P-T diagrams because curves on T-X diagrams often have great curvature or parabolic shapes. See the figure on the right for one example.

Practical Steps for Creating Schreinemakers 'Bundles'

For an n-component system, a) if there are n + 2 phases an invariant point is generated, and b) there are n + 2 univariant curves that radiate from this point, unless one or more of the reactions is degenerate. The first step is to make a list of all possible reactions. The best way to do this is to think about the phases NOT involved, and systematically make a list of reactions and label them by the phases absent.

Click here to learn more about identifying possible reactions...

• As an example, consider the CaO-MgO-SiO₂ system, and the phases wollastonite (Wo), quartz (Qz), diopside (Di), enstatite (En), and akermanite (Ak). 3 components means there are 4 phases in each potential reaction and 5 possible reactions in all: (Wo), (Qz), (Di), (En), (Ak). One is degenerate, leaving:
  1. (Wo) 2Di = Ak+Qz+En
  2. (Di) Ak+Qz = 2Wo+En
  3. (En) Ak+Qz = Di+Wo
  4. (Qz) (Ak) Di = Wo+En

In principle, when creating a Schreinemakers bundle, it doesn't matter which two curves you start with, or which sides you label as the reactants and products of the reactions. However, some starting choices may make the analysis easier than others, so trial and error may be involved. In general, it is best to begin with terminal reactions if you have some. Draw the two reactions intersecting, and label them with products/reactants, and missing phases. If portions of the reaction curves are clearly metastable, make those portions dashed lines at this time.

Show caption

Hide

Two enantiomorphic forms of the same invariant point discussed above. The correct choice cannot be determined without additional knowledge beyond what the the reactions are.

Note: Schreinemakers method will produce bundles of reactions that are topologically correct. Depending on how you orient (label reactants and products) the first two reactions, you can get two different solutions. They will be mirror images of each other. That is, if you go around the invariant point clockwise for one solution, you will hit reactions in the same order as going around the other solution counter-clockwise. The two possibilities are called enantiomorphic projections or enantiomorphic pairs, and one way to think of them is that there is a "right-handed" and a "left-handed" sequence of reactions.

There is no a priori way to determine which of the two is the correct solution. Deciding which is correct requires some geologic intuition and a knowledge of the types of reactions in orienting the Schreinemakers bundles on a phase diagram. For a P-T diagram, for example, high density phases tend to be present on the high pressure side of a reaction. Devolatilization reactions tend to have a steep, positive slope, and the volatiles are liberated on the high T side of the diagram. Additional insight can be gained from thermodynamic principles. The slopes of individual reactions may be calculated using the Clausius-Clapeyron equation.

Once you "fix" the positions of the first two curves, all the other curves will fall into the appropriate sequence. If you find difficulty, try starting with two different curves.

Show caption for Step 1

Hide

We start with two reactions. Their placement and orientation are arbitrary. We indicate the metastable parts of the curves with a dashed line.

Show caption for Step 2

Hide

Now we add another reaction. In this case, the (Di) reaction. We indicate the metastable part with a dashed line. The metastable part of this reaction must be in the upper left quadrant because that is where two "Di" reactions face each other. Anothe way to think of this is that the (Di) reaction, if stable, must take place in the lower right quadrant because it involves Ak-Qz-Wo-En, and those phases can only be stable together in that part of the diagram because of the first two reactions. "Wo En" must be on the right-top side of (Di) because there is another reaction limiting Wo+En. The two must "face" each other, and the angle between them cannot exceed 180°.

Show caption for Step 3

Hide

The invariant point with all four reactions plotted. The metastable extensions are useful because the help determine if we have violated some of the Schreinemakers "rules" listed above.

• Step 1: In our example, Reaction 1 and Reaction 4 are terminal reactions. They are shown plotted in Step 1, above. Their orientation and product/reactant labels have been placed arbitrarily. Metastable portions of the curves are shown dashed.

Now consider an additional reaction. By considering the first two curves, you can determine in which quadrant this new reaction may be stable. Draw the reaction in that quadrant and continue it through the invariant point and out the other side; make the line dashed where metastable. Label each curve with the phase absent, and also label curves with reactants and products on the correct side of each reaction. To place the products and reactants on the correct side of the line, consider the 180° rule, and other hints in notes 1 through 5 above (especially note 5). There is only one correct way to place products and reactants. If you get them reversed, be prepared for confusion and bad juju.

• Step 2: For our example, we will now plot the (Di) reaction. It includes Ak, Qz and En, and it also includes Wo. So, (if it is stable) it can only be stable in the bottom right quadrant. We plot it there and extend it through the invariant point. We label the right hand side "Wo En" because the (Qz)(Ak) reaction also limits Wo+En, and Wo+En cannot be stable more than 180°. Note that the metastable part of this (Di) reaction lies between two curves that eliminate Di, as it should.

Continue to position all additional curves around the invariant point using the conventions above. Label each curve with the phase absent, and also label curves with reactants and products on the correct side of each reaction. In rare instances, you will have to guess how to label the reactions. You continue to the end of the process and check for consistency with the notes above. Generally if you guess wrong, you will find that most of the reactions turn out to be metastable and you do not have a reasonable invariant point.

• Step 3: We add the last reaction. We note that it contains Di, and that means it must be in the upper left quadrant if it is stable (because two other reaction limit Di to that quadrant). This reaction limits the assemblage Ak+Qz and so cannot be more than 180° from (Di). So, we plot it as shown and extend it through the invariant point (where it becomes dashed/metastable). We label the left hand side "Ak Qz" because the (Di) reaction also limits Ak+Qz, and that assemblage cannot be stable more than 180°

Continue adding reactions one-by-one until all are on the diagram. Check for consistency with all the rules listed above. Finally, complete the diagram, if you wish, by adding chemographic drawings showing mineral assemblages in each of the divariant fields.

• Step 4: We now eliminate the metastable reaction extensions as appropriate. This may mean moving some reaction labels to the other side of the invariant point.
• Step 5: Finally, we add the triangular diagrams showing stable mineral assemblages.

Show caption for Step 4

Hide

This is the same as the previous figure, except that we have eliminated metastable reaction extensions.

Show caption for Step 5

Hide

Final diagram with triangular diagrams showing assemblages stable in each field.

Suppose We Have More Than C+2 Phases?

If we are considering a n-component system, and more than n+2 phases, they cannot all exist at a single invariant point. So, there must be multiple invariant points connected by a network of reactions.

Show caption

Hide

This diagram show several possible invariant points in the SiO₂ system and the reactions that emanate from each of them. All Schreinemakers rules are obeyed around each invariant point. The diagram is also consistent with the phase rule. This is a 1-component system. So, three phases coexist at each invariant point, two phases are related by each reaction, and 1 phase is stable in each divariant field.

In this and the following two diagrams, St=stishovite, Co=coesite, aQz=α-quartz, bQz=β-quartz, Trd=tridymite, Cr=cristobalite, and Liq = melt.

Show caption

Hide

The previous diagram is unrealistic because some of the points at the bottom can only exist at negative pressure, and because melting occurs before some of the high-temperature points can be reached. This diagram shows the correct relationships, including the melt (Liq) field. In this diagram, the fields are labeled instead of the reactions. The reactions can be inferred. For example the line separating St and Co must be the St=Co reaction.

Show caption

Hide

Just as some reaction curves are metastable, some invariant points can be metastable, too. This shows an enlargement of the bottom center part of the previous diagram (lines have been extended a bit into negative pressure to show the [Qz] invariant point). The [Cr] invariant point is metastable because it plots in the center of the Cr field. The three reactions that go to the [Cr] invariant point are also metastable.

The drawing above (left) shows phase relationships involving 6 different phases in the SiO₂ system. Only 3 phases may coexist at an invariant point; there are 20 possible invariant points, each involving three of the 6 phases. Only 5 invariant points are shown. The others may exist out of view, or may not exist at all. For demonstration purposes, this diagram has been distorted and extended into negative pressure to include invariant points that do not exist in nature.

The middle diagram above is a "correct" phase diagram showing phase relationships in the SiO₂ system. The invariant point at negative pressure is gone, and a high-temperature melt field is present (creating 3 new invariant points).

We often label reactions by putting the phase absent in normal parentheses. We sometimes label invariant point by putting the phase (or phases) absent in square brackets. The diagram above (right) shows portions of the previous diagram involving β-quartz, cristobalite, tridymite and liquid. Three stable invariant points are shown: [Liq], [β-Qz], and [Trd]. These are the points where NO reactions include liquid, β-quartz, or tridymite. The [Cr] invariant point, between the other 3, is metastable. It is the point where β-quartz, liquid and tridymite would coexist but cannot. They cannot coexist because cristobalite will form instead of any of the other 3.

Concluding Remarks

The beauty of Schreinemakers' Method is that it will always generate a topologically correct "bundle" of reactions for a given set of phases. If you know that two univariant reactions intersect to form an invariant point, then you automatically know the relative positions of all other stable (and metastable) reactions around that invariant point. The slopes of the reaction curves on a pressure-temperature diagram can be determined using the Clapeyron equation. And, because the thermodynamic properties of the phases involved are additive, you only need to obtain thermodynamic data for two reactions to generate the thermodynamic relations of the other reactions. This extends to experimental petrology--experiments need to be completed for only two reactions that intersect at an invariant point--a tremendous savings in time and energy! Application of the method of Schreinemakers is essential to the construction of phase diagrams and pseudosections using modern advanced modeling programs such as Thermocalc, PERPLEX, TWQ and Melts.

For Further Reading

• The classic treatise on Schreinemakers Analysis: E-An Zen (1966) Construction of Pressure-Temperature Diagrams for Multicomponent Systems after the Method of Schreinemakers -- A Geometric Approach. U.S. Geol. Surv. Bull. 1225, 56p.
• See also: John Winter (2001), An Introduction to Igneous and Metamorphic Petrology, Prentice Hall, pages 527-530 for an additional description and examples of the Method of Schreinemakers.

Teaching Activities and Problem Sets

• Schreinemakers Problem #1 - This is a fairly basic Schreinemakers problem: identifying the sequence of stable and metastable reactions around two invariant points. The phases involved include diopside, merwinite, akermanite, montecellite, forsterite and wollastonite. There are few reactions, the reactions are easy to balance, and determining stability/metastability is straightforward. The exercise comes from Dexter Perkins.
• Schreinemakers Problem #2 - This is a standard Schreinemakers problem: identifying the sequence of stable and metastable reactions around an invariant point. Phases involved include pyrope, spinel, enstatite, sillimanite, and cordierite. The exercise comes from Dexter Perkins.
• Schreinemakers Problem #3 - This is a standard Schreinemakers problem: identifying the sequence of stable and metastable reactions around an invariant point. The phases involved include anorthite, grossular, CaTs, kyanite, and quartz. The added twist is that this problem requires calculating the volume and entropies of reaction, and use of the Clausius-Clapeyron Equation, so that the slopes of the reaction curves are correct, and so that the correct enantiomorph solution is found. The exercise comes from Dexter Perkins.
• Schreinemakers Problem #4 - This, in principle, is a standard Schreinemakers problem: identifying the sequence of stable and metastable reactions around an invariant point. However the system and phases (margarite, zoisite, anorthite, grossular, prehnite, kyanite) are complicated, reactions are hard to balance, and this problem can be quite difficult for some students. The exercise comes from Dexter Perkins.
• Controls on Mineral Assemblages Lab (Microsoft Word 32kB Mar29 07) - This one week exercise, provided by Dave Pattison at the University of Calgary, includes problems sets involving Schreinemakers' analysis, bulk compositions and mineral assemblages.