For the Instructor
These student materials complement the Modeling Earth Systems Instructor Materials. If you would like your students to have access to the student materials, we suggest you either point them at the Student Version which omits the framing pages with information designed for faculty (and this box). Or you can download these pages in several formats that you can include in your course website or local Learning Managment System. Learn more about using, modifying, and sharing InTeGrate teaching materials.Unit 9 Reading: The Global Carbon Cycle
by David Bice, The Pennsylvania State University
Carbon is unquestionably one of the most important elements on Earth. It is the principal building block for the organic compounds that make up life. Carbon's electron structure enables it to readily form bonds with itself, leading to a great diversity in the chemical compounds that can be formed around carbon; hence the diversity and complexity of life. Carbon occurs in many other forms and places on Earth; it is a major constituent of limestones, occurring as calcium carbonate; it is dissolved in ocean water and fresh water; and it is present in the atmosphere as carbon dioxide, the second most abundant greenhouse gas and arguably the most important climate forcing.
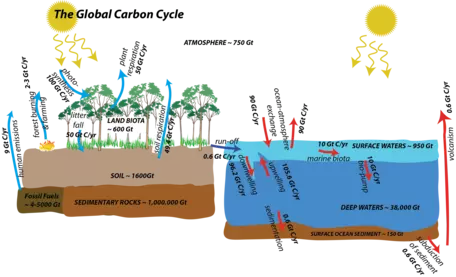
The flow of carbon throughout the biosphere, atmosphere, hydrosphere, and geosphere is one of the most complex, interesting, and important of the global cycles. More than any other global cycle, the carbon cycle challenges us to draw together information from biology, chemistry, oceanography, and geology in order to understand how it works and what causes it to change. The major reservoirs for carbon and the processes that move carbon from reservoir to reservoir are shown in Figure 1 below. You do not need to understand this figure yet, but just appreciate that there are many reservoirs and a lot of processes that exchange carbon — the carbon cycle is anything but simple! We will discuss these processes in more detail below and then we will construct and experiment with various renditions of the carbon cycle.
Our eventual goal is to create a global carbon cycle model that is good enough to be used for future projections that we can have some confidence in. In other words, if we "force" the model through a combination of land use changes and fossil fuel burning, we would like to have a model that gives us believable results. How do we know if the results are believable? We do this by testing our model against the historical record of human forcings and the known history of atmospheric CO2 concentration and then "tuning" our model until it matches the historical observations. But to get to this point, we have to consider all of the parts of the global carbon cycle and include them in the model.
![[creative commons]](/images/creativecommons_16.png)
Carbon Dioxide Through Time
The global carbon cycle is currently a topic of great interest because of its importance in the climate system and also because human activities are altering the carbon cycle to a significant degree. The potential effects of human activities on the carbon cycle, and the implications for climate change, were first noticed and studied by the Nobel Prize-winning Swedish chemist Svante Arrhenius in 1896. He realized that CO2 in the atmosphere was an important greenhouse gas and that it was a by-product of burning fossil fuels (coal, gas, oil). He even calculated that a doubling of CO2 in the atmosphere would lead to a temperature rise of 4-5 °C — amazingly close to the current estimates obtained with global, 3-D climate models that run on supercomputers. This early recognition of human perturbations to the carbon cycle and the climatic implications did not raise many eyebrows at the time, but humans' "experiment" adding massive amounts of CO2 to the atmosphere was just beginning then.
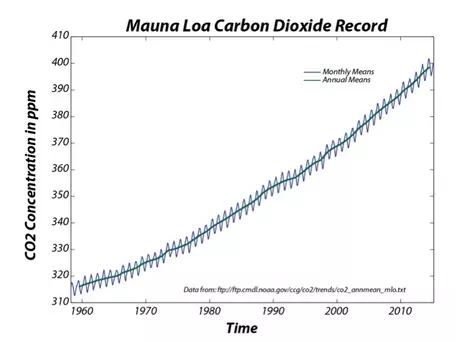
In the late 1950s, Roger Revelle, an American oceanographer based at the Scripps Institution of Oceanography in La Jolla, California, began to ring the alarm bells over the amount of CO2 being emitted into the atmosphere. Revelle was very concerned about the greenhouse effect from these emissions and was cautious because the carbon cycle was not then well understood (some researchers thought that the oceans would absorb most of this excess CO2), so he decided that it would be wise to begin monitoring atmospheric concentrations of CO2. In the late 1950s, Revelle and a colleague, Charles Keeling, began monitoring atmospheric CO2 at an observatory on Mauna Loa, on the Big Island of Hawaii. Mauna Loa was chosen because its elevation and location away from industrial centers made the values measured there as close to a global signal as any other location. The record from Mauna Loa (Fig. 2), one of the classic plots in all of science, is a dramatic sign of global change that captured the attention of the whole world because it shows that this "experiment" we are conducting is apparently having a significant effect on the global carbon cycle. The climatological consequences of this change are potentially of great importance to the future of the global population. The CO2 concentration recently crossed the 400 ppm mark for the first time in millions of years!
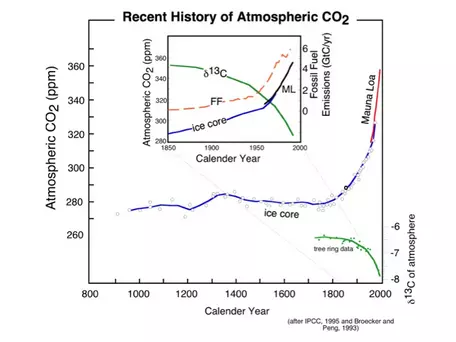
As the Mauna Loa record and others like it from around the world accumulated, a diverse group of scientists began to appreciate Revelle's concern that we really did not know much about the global carbon cycle that ultimately regulates how much of our CO2 emissions stay in the atmosphere. The importance of present-day changes in the carbon cycle, and the potential implications for climate change, became even more apparent when scientists began to get results from studies of gas bubbles trapped in glacial ice. As you may have learned, the bubbles are effectively samples of ancient atmospheres, and we can measure the concentration of CO2 and other trace gases like methane in these bubbles. Then, by counting the annual layers preserved in glacial ice, we can date these atmospheric samples, providing a record of how CO2 changed over time in the past. Figure 3 shows the results of some of the ice core studies relevant for the recent past — back to the year 900 A.D.
![[creative commons]](/images/creativecommons_16.png)
![[creative commons]](/images/creativecommons_16.png)
The striking feature of these data is that there is an exponential rise in atmospheric CO2 (and methane, another greenhouse gas) that connects with the more recent Mauna Loa record to produce a rather frightening trend. Also shown in Figure 3 is the record of fossil fuel emissions from around the world, which shows a very similar exponential trend. Notice that these two data sets show an exponential rise that seems to begin at about the same time. What does this mean? Does it mean that there is a cause-and-effect relationship between emissions of CO2 and atmospheric CO2 levels? Although we should remember that science cannot prove things to be true beyond all doubt, it is highly likely that there is a cause-and-effect relationship. We can use the δ13C value of the CO2generated from the combustion of fossil fuels as a sort of fingerprint for the extra CO2 in the atmosphere. This allows us to say, with a great deal of certainty, that the observed rise in atmospheric CO2 and the emissions of CO2 are in fact related and are due to human activities.
How serious is our modification of the natural carbon cycle? Here, we need a slightly longer perspective from which to view our recent changes, so we return to the records from ice cores and look further back in time (Fig. 4).
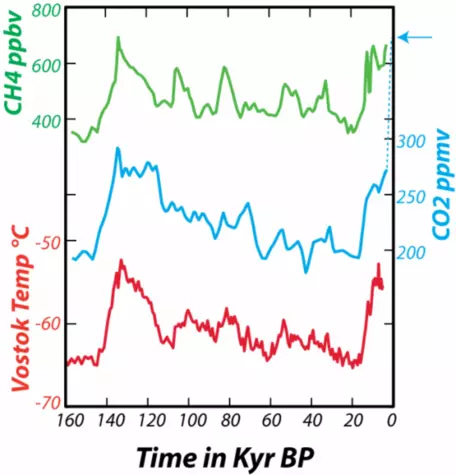
In addition to providing a record of the past concentration of CO2 in the atmosphere, the ice cores also give us a temperature record. By studying the ratios of stable isotopes of oxygen that make up the glacial ice, we can estimate the temperature (in the region of the ice) at the time the snow fell (glacial ice is formed by the compression of snow as it gets buried to greater and greater depths). From these data, shown in Figure 5, we can see the natural variations in atmospheric CO2 and temperature that have occurred over the past 160,000 years (160 kyr).
![[reuse info]](/images/information_16.png)
![[creative commons]](/images/creativecommons_16.png)
In fact, looking at this long span of time enables us to see clearly that the present CO2 concentration of the atmosphere is unprecedented in the last several hundreds of thousands of years. As geoscientists, we are interested in more than just the last few hundred kiloyears, so we look back into the past using sediment cores retrieved from the deep sea. Geochemists studying these sediments have been able to reconstruct the approximate concentration of CO2 in the atmosphere.
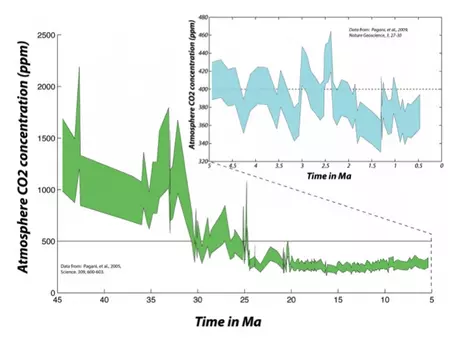
To find atmospheric CO2 levels equivalent to the present, we have to go back 2.5 million years (to the late Pliocene, Fig. 6). This means that, to the extent that the state of the carbon cycle is closely linked to the condition of the global climate, we are pushing the system toward a climate that has not occurred anytime within the last several million years — not something to be taken lightly, especially considering that Earth was much warmer then and sea level was between 10and 20 m higher than today!
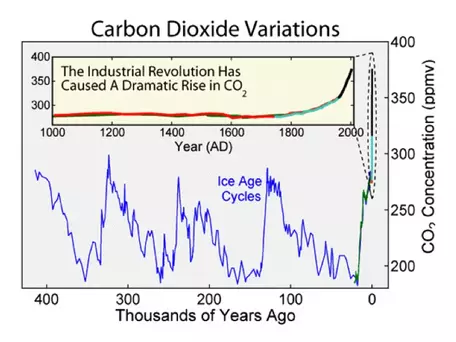
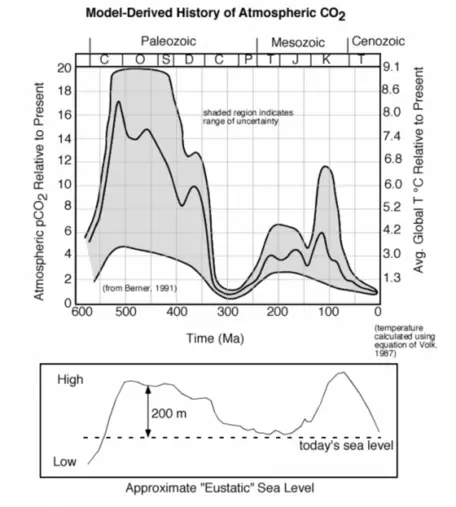
The further back in time we go, the more difficult it is to figure out how CO2 concentrations have changed, but that has not stopped some from attempting (Fig. 7).
One thing that seems clear is that further back in time, CO2 levels were much, much higher, and the average global temperature was also much higher. Why has the CO2 concentration changed so much over geologic time? This is a big question whose answer involves many factors, including changes in plate tectonics, the terrestrial biosphere, and variations in the burial of carbon in ocean sediments, which is probably the biggest factor. Sea level was much higher during the two big peaks in CO2 — probably due in part to changes in plate tectonics. Higher sea level decreases the planet's albedo, making it warmer. A warmer ocean cannot absorb atmospheric CO2 and instead releases the gas to the atmosphere, setting up a positive feedback mechanism.
In conclusion, from this brief look at the record of fossil fuel emissions and atmospheric CO2 concentrations, it is clear that we have cause for concern about the effects of the global CO2 "experiment." Because of this concern, there is a tremendous effort underway to better understand the global carbon cycle. In the remainder of this module, we will explore the global carbon cycle by first examining the components and processes involved and then by constructing and experimenting with a variety of models. The models will be relevant to the dynamics of the carbon cycle over a period of several hundred to a few thousand years — these models will enable us to explore a variety of questions about how the system will behave in our lifetimes and a bit beyond.
![[creative commons]](/images/creativecommons_16.png)
![[creative commons]](/images/creativecommons_16.png)
Overview of the Carbon Cycle From the Systems Perspective
The global carbon cycle is a whole system of processes that transfers carbon in various forms through Earth's different parts. The carbon that is in the atmosphere in the form of CO2 and CH4 (methane) does not stay there for long — it moves to other places and takes different forms. Plants use the CO2 from the atmosphere in photosynthesis to make carbohydrates and other organic molecules, and from there it may return to the atmosphere as CO2 or it may enter the soil as still different compounds that contain carbon. Some carbon is deposited in sedimentary rocks originating in the oceans, and much later, this carbon may be released to the atmosphere via weathering. So carbon moves around — it flows — from place to place.
Because CO2 is such an important greenhouse gas, the way the carbon cycle works is central to the operation of the global climate system. Later in this module, we will work with a computer model of the cycle to do experiments that will help us understand how it works, but it will help to begin with an overview from the systems perspective. What do we mean by a systems perspective? These words just mean that we focus on the places where carbon resides (the reservoirs, in systems terminology), how it moves from reservoir to reservoir, how much of it moves from place to place, and what controls those movements. This same perspective has been behind all of the models we have worked with in this class.
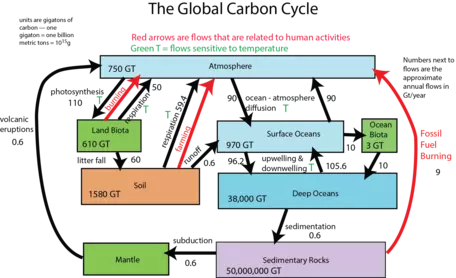
First, let us consider the main reservoirs of carbon. These can be seen in the diagram below (Fig. 8), where each box represents a different reservoir. Remember that in each of them, the carbon may be in very different forms. For example, carbon in the atmosphere may be found as carbon dioxide or methane, whereas carbon in the biosphere is found in organic molecules, and carbon in rivers and streams is most commonly found as bicarbonate anion (HCO3-). Note: a Gt or gigaton is a billion metric tons or 1015 grams, which is a whole lot of carbon!
The mantle reservoir is huge and somewhat removed from the other reservoirs, thus we will not really bother with it. Among the other reservoirs shown in Figure 8, you can see that there is a huge range in size. The ocean biota contain a very small amount of carbon relatively speaking, while sedimentary rocks contain a vast quantity (in the form of calcite — CaCO3 — that forms limestones, as well as in coal, petroleum, and organic rich shales).
Now let us look at the system with flows included, as arrows connecting the reservoirs (Fig. 9). The black arrows represent natural processes of carbon transfer, while the red arrows represent changes humans are responsible for. The magnitudes of the flows are shown in units of gigatons of carbon per year. The diagram as constructed here represents a steady state if we just consider the black arrows; the flows going into each reservoir are equal to the flows going out of the reservoir — in other words, there is a balance. We will step through this system, talking about the processes involved in the flows, but first, let us try to learn something from the numbers themselves in this diagram.

![[creative commons]](/images/creativecommons_16.png)
![[creative commons]](/images/creativecommons_16.png)
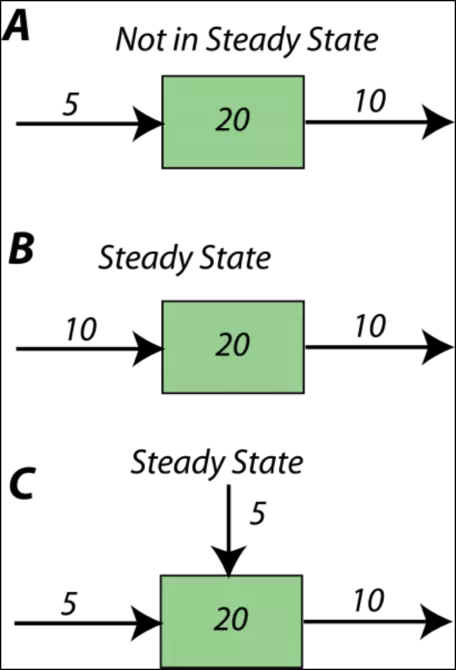
First, a short digression to better understand the notion of steady state. Figure 10 illustrates some simple systems, one of which is not in a steady state, and the others of which are. In the first example, A, more material (10 units per time) is subtracted from the reservoir than is added (5 units per time), and so over time, the amount of material in the reservoir will decline — it will not remain constant, or steady. In each time step, the reservoir will lose 5 units of whatever the material is. In the other two examples (B,C), the amount added is the same as the amount subtracted, so these reservoirs will be in a steady state. If you look at example C, you see that the sum of inflows (5+5) is equal to the outflow (10).
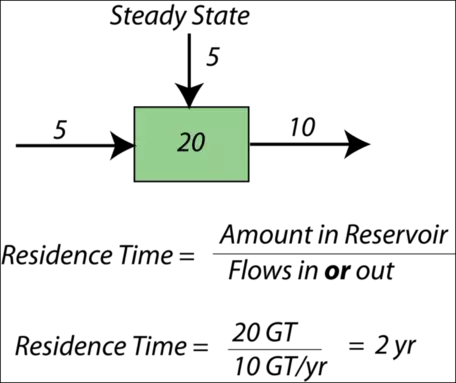
When a system is in a steady state, we can say something about the average time the material will spend in the reservoir — this is called the residence time for the reservoir. Here is a simple example — if there are 40,000 students at Penn State, and 10,000 students enter each year and 10,000 students graduate each year, then the system is in a steady state. The residence time is the total number of students divided by either the number entering or graduating each year — this gives four years as the average residence time. Figure 11 illustrates this concept graphically.
![[creative commons]](/images/creativecommons_16.png)
![[creative commons]](/images/creativecommons_16.png)
The concept of residence time is a useful one in studying any kind of system because it tells us something about how quickly material is moving through a system, and more importantly, it tells us how quickly some part of the system, or the system as a whole, can respond to changes. If something has a short residence time, it can respond quickly to changes, whereas if it has a long residence time, it responds very slowly. The residence time is closely related to the response time, which as the name implies, is a measure of how much time it takes for a system to respond to a change. The word "respond" in this context means "return to a steady state." In very simple systems (e.g., one reservoir with an inflow and an outflow), the response time and residence time are the same, but in more complex systems with connected reservoirs, the response time is generally not the same as the residence time.
Although the residence time and the response time are often (but not always) the same value, they represent different ideas. As we said earlier, the residence time is a measure of the average length of time some material spends in a reservoir — like the average length of time a carbon atom spends in the atmosphere. The response time, on the other hand, is a measure of how quickly something returns to steady state after some disturbance that knocks the system out of steady state. So response time is only meaningful in cases where a system has a tendency to remain in a steady state.
Now, let us turn to the carbon cycle and consider some of the flows in and out of the reservoirs. What is the residence time for the atmosphere? To determine this, we take the amount in the reservoir (750 Gt) and divide it by the sum of the inflows or the outflows. Let us take the outflow: 100 Gt C/yr for photosynthesis plus 90 Gt C/yr going into the oceans. The residence time is thus:
Residence time = ` tau = (750 Gt)/(190 Gt yr^-1) = ` 3.9 yearsThis is a pretty short residence time. Now, let us look at the deep ocean (which is the vast majority of the oceans) — its residence time is:
Residence time = ` tau = (38,000 Gt)/(106.2 Gt yr^-1) = ` 358 yearsThe result, 358 years, which means that on average, an atom of carbon will spend 358 years in that reservoir. But if we think about the oceans as a whole, ignoring the internal cycling and assuming that the net exchange between the surface ocean and the atmosphere tends to be very close to zero, we see that there is a flow of 0.6 GtC/yr coming in via rivers, and 0.6 GtC/yr going out via sedimentation. In this case, the residence time for carbon in the oceans would be:
Residence time = ` tau = (38,973 Gt)/(0.6 Gt yr^-1) = ` 64,965 yearsThis result is much longer than the atmosphere, and what this tells us is that the carbon cycle has some parts that respond quickly, but other parts that respond very slowly; the very slow parts tend to put a damper on how quickly the other parts can change. In other words, if we suddenly inject carbon dioxide into the atmosphere, you might think that the short residence time of the atmosphere means that the excess CO2 can be removed very quickly, but because these reservoirs are linked together, it turns out that the ocean must return to its steady state before the atmosphere can get back to its steady state.
A Simple Analogy
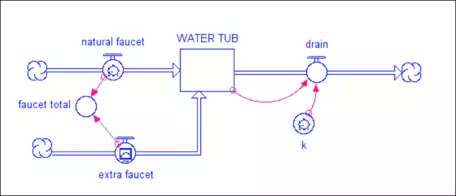
![[creative commons]](/images/creativecommons_16.png)
One faucet represents the natural addition of water to the tub, while the other represents a new flow. The tub has a drain in it that takes out 10% of the water in a given time interval (the value of k is 0.1 and the drain flow is just the amount in the tub times k). If the extra faucet is initially set to zero, this system will find a steady state in which the faucet and drain are equal, so the amount in the reservoir remains constant. What would happen to the system if you increase the faucet flow once it is in its steady state? If the faucet flow increases, then the system will find a new steady state, but one with more water in the tub. At steady state, you can write a simple equation that says:
F = k*W
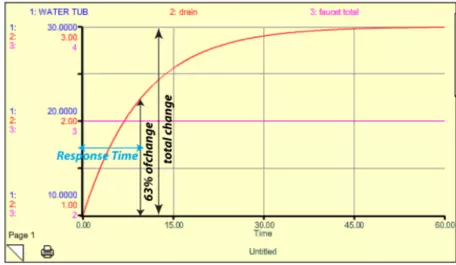
Here, F is the flow rate, k is the rate constant (0.1 in this case), and W is the amount of water in the tub. It turns out that the response time for this system is just 1/k. In this example model, k = 0.1 so the response time is 10 time units (the units depend on how the flows are given — liters per second or minute). This response time is not the length of time required for the system to get into a steady state — it is the time required to accomplish 63% of the change to the new steady state. Why 63%? There is some math behind this choice, but in essence it is just a convention that helps us avoid the problem of picking the time when steady state is achieved, which is difficult since the system does so asymptotically. Figure 13 shows how this looks. In the figure, the blue line for the water tub is hidden beneath the red curve of the drain — these have different scales on the left-hand side, but they are the same exact shape, so one plots over the other.
![[creative commons]](/images/creativecommons_16.png)
I changed the faucet here to 3, and the water in the tub rose until it reached a value of 30, where the drain value then became equal to the faucet value and the system reached a new steady state. As shown by the blue arrow, it takes 10 time units to accomplish 63% of the change.
So, this is a system that has a negative feedback (the drain) that drives it to a steady state, which means that regardless of the values of the faucet or the drain constant, k, the system will find a steady state.
In Figure 14, you see what happens if we turn the extra faucet on for a bit and then turn it off.

![[creative commons]](/images/creativecommons_16.png)
The system gets thrown out of its steady state temporarily, but returns to the original steady state when the extra faucet is turned back off. Note that there is a lag time here — the water tub peaks about 5 time units after the faucet peaks (this is the sum of the two faucets). If we were to decrease k, then the response time would lengthen, and the lag time would also lengthen. Think of this spike in the extra faucet as being equivalent to a short-term addition of CO2 into the atmosphere. But what if we turn the extra faucet on and then leave it on for some time at a steady rate? This might be equivalent to us adding CO2 to the atmosphere and then keeping those emissions constant (sometimes referred to as the "stabilization" of emissions). We can simulate this scenario with our simple model, and the results are shown in Fig. 15.
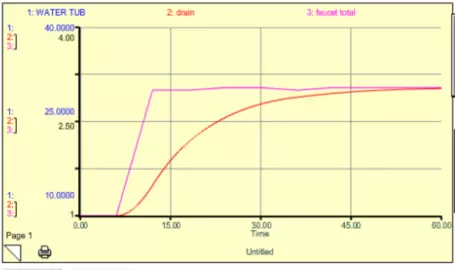
![[creative commons]](/images/creativecommons_16.png)
What you see is that the system responds by increasing the water in the tub until a new steady state is reached. The length of time needed to achieve the new steady state is determined by the response time of the system, which again, is governed by the magnitude of the drain constant, k.
In the real carbon cycle, this response time is measured in tens of thousands of years. For example, remember that the residence time of the deep ocean is about 3,800 years. The response time of the whole carbon cycle must be much longer than this because CO2 emissions are cycled through more than just the deep ocean. Unfortunately you cannot add up the residence time of the individual reservoirs to get the response time of the whole carbon cycle, which is really what we want to know, because the system is much more complex than this. The natural carbon cycle will find a new steady state (it will "stabilize") in response to our carbon emissions, but it will take many thousands of years to do so. In the meantime, the system will continue to change as it makes this adjustment.
Now that we are done with this digression, let us turn our attention back to learning about the different components of the carbon cycle.
The Terrestrial Carbon Cycle
In Figure 8, we showed the different reservoirs that hold carbon on Earth. Figure 9 added flow arrows to show how carbon moves between these reservoirs, but did not present the details of how the element migrates from one place to another. To fully understand the carbon cycle and how we might model it requires getting into the nitty-gritty, and we will start with the terrestrial realm, through which carbon moves via five main processes represented as blue arrows in Figure 16. We will explore these processes below, beginning with photosynthesis.
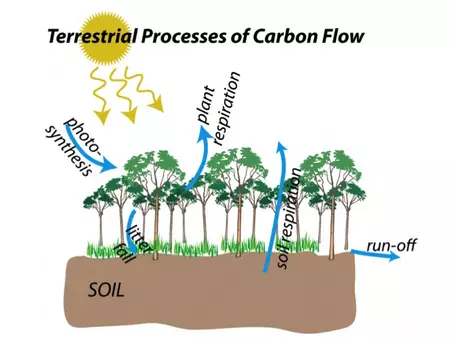
![[creative commons]](/images/creativecommons_16.png)
Photosynthesis
Since its origin over 3 billion years ago, photosynthesis has been one of the most important processes on Earth, helping to make our planet habitable, in stark contrast to the other planets in our solar system. The basic idea is that plants capture light energy and use it to convert water molecules and carbon dioxide into carbohydrates, which are used for fuel and construction of plant tissues. Oxygen, which is crucial to making Earth habitable for animals, is a by-product of this reaction, which is summarized as follows:
6CO2 (Carbon dioxide) + 6H2O (Water) ---> C6H12O6 (Sugar) + 6O2(Oxygen)
Photosynthesis takes place in the chloroplasts located in the interiors of leaves (Fig. 17). Here, chlorophyll absorbs solar energy in the red and blue parts of the visible light portion of the electromagnetic spectrum.
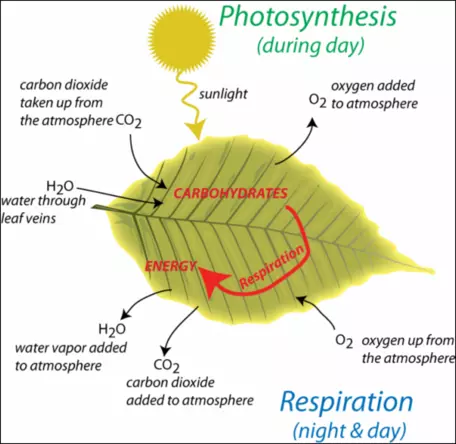
![[creative commons]](/images/creativecommons_16.png)
Photosynthesis is one of the most important processes in the carbon cycle, in part because it is so powerful. This power can be seen in the annual cycle of atmospheric CO2 concentration (Fig. 2). When the northern hemisphere growing season begins in the spring, the atmospheric pCO2 drops rapidly, rebounding at the end of fall when most northern hemisphere plants become dormant. It is as if the land biota are collectively breathing in during the growing season and then breathing out during the winter months. The northern hemisphere growing season dominates the atmospheric pCO2 record because the northern hemisphere has a greater amount of land area covered by vegetation (especially forest) than the southern hemisphere.
The rate of consumption of CO2 by photosynthesis is mainly a function of water availability, the concentration of CO2 in the atmosphere, temperature, and key nutrients such as nitrogen. The importance of water in plant growth is obvious from looking at the equation above. The fact that photosynthesis depends on the concentration of CO2 in the atmosphere is not obvious, but is very important. Plants take in CO2 through small openings (about 10 microns in diameter) in their leaves called stomata, which they can control like valves, opening and closing to adjust the rate of transfer. The more CO2 they let in, the faster the rate of photosynthesis and the faster the growth — but if plants open their stomata wide to let in a lot of CO2, they can lose a lot of water, which can cause problems. If there is a greater concentration of CO2 in the atmosphere, then plants can get a good dose of CO2 by opening their stomata just a little bit, allowing them to conserve water. What this amounts to is increased efficiency of growth at higher levels of CO2. We call this effect CO2 fertilization, and it is an important way in which plants are our friends in helping to minimize the rise of CO2 in the atmosphere associated with fossil fuel combustion. You can see this effect in Figure 18 below, which shows the theoretical relationship between the CO2 concentration in the atmosphere and the uptake of carbon from photosynthesis by land plants, summed up for the whole globe. In reality, the actual response is generally less than this theoretical response because of limitations to growth from other nutrients that plants need. Note that there is an upper limit to this effect; at high levels of CO2, plants do not respond as readily to additional increases in atmospheric CO2. Likewise, there is a lower limit to photosynthesis imposed by CO2 levels, but we are not likely to approach such low levels in the next billion years or so (we will eventually have this problem since atmospheric CO2 is slowly being drawn down through the precipitation of limestone).
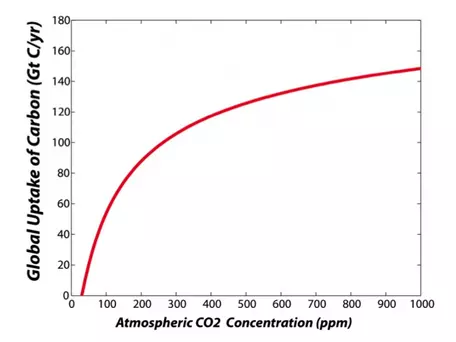
![[creative commons]](/images/creativecommons_16.png)
Temperature is another important consideration in many life processes, and photosynthesis is no exception. As a general rule, the rates of most metabolic processes increase with temperature, but there is usually an upper limit where high temperatures begin to destroy important enzymes or otherwise inhibit life functions (recall the temperature-dependent growth function in our Daisyworld exercise). For the majority of plants, this upper limit is not likely to come into play given the kinds of temperature changes we might expect in the space of a couple hundred years, so we will safely ignore it in our modeling efforts today (if our model does lead to temperature changes greater than 10-20 °C in a hundred years, we would presume that there is some problem with the model as this is unrealistic behavior). Another important reason to take temperature into account in our model of photosynthesis is that it turns out that in most environments, an increase in temperature correlates with an increase in precipitation, and since many regions where plants grow are somewhat limited by water, especially toward the end of the growing season, increased precipitation would lead to a greater yearly rate of photosynthetic uptake of atmospheric carbon.
How can we keep track of changing temperatures in our model of the carbon cycle? Recall from our earlier modeling exercise on Earth's energy balance with the sun that an increase in atmospheric CO2 leads to an increase in the greenhouse effect and thus a warmer planet. One option is that we could attach our model of the carbon cycle to one of the models of the climate system we made a few weeks ago. Another option would be to develop a simple relationship based on the known history of atmospheric CO2 and global temperature. This has been done by a variety of people (e.g., Walker, 1991), and the result is an equation that looks like this:
` DeltaT = 2.5*(ln((pCO_2)/290))/(ln(2)) ` °C where ` DeltaT ` is the temperature difference, in °C, between the start of a model simulation and any time thereafter; ln is the natural log; pCO2 is the concentration of CO2 in the atmosphere in ppm (parts per million); and 290 is the concentration (ppm) of CO2 in the atmosphere around 1890, when our model would be set to begin. In this way, we could monitor Earth's temperature relative to the starting temperature (14 °C) it had at the beginning of the industrial revolution. This logarithmic relationship means that for each doubling of CO2, there is a 2.5 °C temperature increase.Next, we must consider the problem of how to describe photosynthesis globally, in the form of an equation that we can use in our model. We get some help here from studies on a variety of different plants grown in greenhouses with varying levels of CO2 and varying temperatures. We should realize, of course, that there are always uncertainties that arise when transferring results from the laboratory to the real world, and there are even more problems when one tries to extrapolate to the scale of the whole world. The truth of the matter is that we do not yet know enough about the operation of our whole planet to solve this problem with confidence — the study of the global carbon cycle is still in its early stages. Still, if we do not make some attempt to describe this process in the form of a global model, our understanding of the dynamics of the global carbon cycle will languish in the early stages, so we forge ahead.
The accumulated results of decades of scientific study indicate that our function for photosynthesis should satisfy the following characteristics:
- The present day global flow should be 120 Gt C/yr (one gigaton of carbon per year; 1 Gt = 1015g, also known as a petagram, Pg).
- The rate should increase at higher atmospheric CO2 levels, but there should be a saturation point, where additional increases in atmospheric CO2 yield no further increase in the rate of photosynthesis.
- The rate should increase with increasing temperature.
There are several ways to construct an equation that incorporates this information, but in our modeling exercise, we will use the following equations, adapted from Gifford (1993):
` F_p = ((P_(max)*pCO2_(eff))/(K_(hs) + pCO2_(eff))) * (1 + (Tsens_p*DeltaT)) ` ` P_(max) = ((K_(hs) + (pCO2_("init") - pCO2_(min)))*F_(P,"init"))/((pCO2_("init") - pCO2_(min)) )`where,
Fp is the global rate of photosynthetic uptake of CO2 in Gt C/yr.
Pmax is a parameter with units of GtC/yr that is used to force the equation for Fp to give the proper value corresponding to the starting conditions of the model.
Khs = 72.5 ppm — the half-saturation value — the atmospheric CO2 concentration at which the rate of photosynthesis, Fp, is half of the ultimate saturation value (this is independent of temperature, but the temperature does come into play in the second part of the equation).
pCO2init = 290 ppm — the pre-industrial (1880) atmospheric CO2 concentration
pCO2min = 30 ppm — value below which no photosynthesis can occur
pCO2eff = pCO2 - pCO2min— the effective atmospheric CO2 concentration
Fp,init = 100 GtC/yr — the initial (pre-industrial) value for global photosynthesis
Tsensp = 0.04 — establishes the increase of Fp per degree of warming
`DeltaT` = T - Tinit — temperature difference relative to initial temperature. Tinit is set to 0Khs is a key parameter in defining the shape of the curve, which is always constrained to give a photosynthesis rate of 100 Gt C/yr when the atmospheric CO2 concentration is 290 ppm — the starting (~1890) value.
The formulation here gives an increase in photosynthesis by a factor of 1.4 if the temperature increases 10 °C. This is sometimes called the Q10 for the process, and a Q10 of 1.4 is in line with a variety of observations from experiments in greenhouses. It is important to note once again that there is an upper limit to this temperature sensitivity function in the real world, but we do not expect to approach it in this modeling exercise, so we will not try to incorporate it into our equation.
Defined in the manner outlined above, our photosynthesis flow is the same as what is commonly called Gross Primary Production. Gross Primary Production (GPP) differs from Net Primary Production (NPP), which is the gross minus respiration.
Plant Respiration
If we think of photosynthesis as the process of making fuel (carbohydrates), then respiration can be thought of as the process of burning that fuel — using it for maintenance and growth. This process can be described in the form of a reaction, just like photosynthesis. That reaction is:
C6H12O6 + 6O2 --> 6CO2 + 6H2O + energy
which is effectively the reverse of photosynthesis.
Through respiration, plants (and animals) release water and carbon dioxide, and they use up oxygen. Do the carbon flows involved in respiration and photosynthesis balance each other as the equations seem to imply? The answer is no — otherwise, how could organisms grow?
Experiments on a variety of plants indicate that the ratio of photosynthesis to respiration is generally about 2 to 1. When plants are young, and growing rapidly, but with not much biomass to maintain, this ratio is even higher; in older, larger plants, this ratio is lower since more carbon needs to go towards maintenance.
For the purposes of our model, we will assume that the global collection of plants has a photosynthesis to respiration ratio of about 2 to 1, so we will formulate plant respiration in the following manner:
Fpr = Fp * (0.5)
where Fpr is the rate of global plant respiration in Gt C/yr and Fp is the rate of global photosynthesis by land plants.
Litter Fall (and below-ground addition to the soil)
Dead plant material enters the soil in two ways — it falls on the surface as litter, and it is contributed below the surface from roots. The relative importance of these two pathways into the soil varies according to the plants in an ecosystem, but it appears that the two are commonly about equal, which may seem a bit surprising, but loss of organic carbon from root systems is a process that we generally do not see. The flow of carbon associated with litter fall is roughly the difference between the photosynthetic uptake of carbon and the return of carbon through plant respiration. If this were not the case, then the size of the global land biota reservoir would be growing or declining, and although some regions are growing, others are shrinking, and they nearly balance out.
Having already chosen the initial rates for photosynthesis and plant respiration, at 100 and 50 Gt C/yr (see Photosynthesis and Plant Respiration sections above), this leaves us with a value of 50 Gt C/yr for the rate of carbon added to the soil reservoir through the process of litter fall. In our model, we do not want this parameter to have a constant value, however. Litter fall would undoubtedly change as a function of the size of the land biota reservoir. So, we can define the litter fall flow (Flf) in the form of a standard draining flow:
Flf= land_biota * (50/INIT(land_biota))
where Flf is the flow in Gt C/yr and land_biota is the amount of carbon stored in the land biota reservoir at any given time.
Soil Respiration
In addition to plant metabolic processes, respiration (sometimes called decay) also occurs within the soil, as microorganisms consume dead plant material. In terms of a chemical formula, this process is the same as described above for plants (the reverse of photosynthesis).
There is an unseen but fascinating universe of microbes living within the soil, and they are the key means by which nutrients such as carbon and nitrogen are cycled through the soil system. A great diversity of microorganisms live in the soil, and they are capable of consuming tremendous quantities of organic material. Much of the organic material added to the litter or within the root zone each year is almost completely consumed by microbes; thus there is a reservoir of carbon with a very fast turnover time — on the order of 1 to 3 years in many cases. The by-products of this microbial consumption are CO2, H2O, and a variety of other compounds collectively known as humus, which is not the same as hummus, the Mediterranean chickpea puree! Humus is a much less palatable compound, as far as microbes are concerned, and is not decomposed very quickly. After it is produced at shallow levels within the soil, it generally moves downward and accumulates in regions of the soil with high clay content. Part of the reason it accumulates in the lower parts of the soil is that there tends to be less oxygen in that environment, and the lack of oxygen makes it even more difficult for microbes to work on this humus and decompose it. However eventually, due to various processes (animals burrowing, people plowing, etc.) that stir the soil, this humus moves back up to where there is more oxygen, and the microbes eventually destroy it and release some more CO2. Humus therefore constitutes a long-lived reservoir of carbon in the soil. Carbon 14 (14C) dates on some of this soil humus give ages of several hundred to a thousand years old. Taken together, the fast and slow decomposition processes, both driven by microbes, lead to an average carbon residence time of around 20 to 30 years for most soils. The data used in our global carbon cycle model lead to a residence time of about 26 years for the global soil carbon reservoir.
Soil microbes (considered in terms of their respiratory output) are very sensitive to the organic carbon content of the soil as well as its temperature and water content, respiring faster at higher carbon concentrations, higher temperatures and in moister conditions. Studies seem to indicate that soil respiration is in fact even more sensitive to temperature than photosynthesis and plant respiration. In general, higher temperatures tend to correspond with higher rates of precipitation, so we can consider the effects of water to go hand in hand with temperature. In our model of the carbon cycle, we will use an expression for soil respiration (modified slightly from Kwon and Schnoor, 1994) that takes these observations into account:
` F_(sr) = Soil * (49.4/(INIT(Soil)))*(1 + (Tsens_(sr)*DeltaT)) ` ` Tsens_(sr) = 0.10 ` to `0.01 `The temperature sensitivity part of the equation is a linear function like that used in defining photosynthesis. The Tsenssr value of 0.1 gives an increase in soil respiration by a factor of 2.0 if the temperature increases 10 °C. This gives a Q10 of 2.0 and is in line with a variety of observations (which generally are not in close agreement; this is not a well-constrained part of the model). In our initial model, we will set this value to be 0.03, because it gives a better match with the observed record of atmospheric CO2. It is important to note once again that there is an upper limit to this temperature sensitivity function in the real world, but we do not expect to approach it in this modeling exercise, so we will not try to incorporate it into our equation.
Permafrost — an Unknown
In recent years, increasing attention has been directed at permafrost soil carbon since the polar regions are warming much faster than the rest of the globe. As the permafrost melts, carbon that was added to these soils, by processes like litter fall, will become available for soil microbes to respire and release to the atmosphere. In fact, this process is almost surely happening already, but given that much of the permafrost is still frozen, we have probably not seen the real manifestation of this source of carbon. Estimates are variable, but a figure like 1000 to 1500 Gt of carbon reflects the current thinking of how much carbon is locked up in permafrost; this is a huge amount and has the potential to significantly alter future atmospheric CO2 levels. As the permafrost begins to melt, some estimates are that it will contribute 2-5 Gt C/yr, which is large compared to human-related inputs. Of course, some of this released carbon will be offset by new carbon stored in shrubs and small trees that will expand in warmer temperatures, but initially, the system will not be in equilibrium, and permafrost regions can be expected to be a net source of CO2 to our atmosphere.
The process of permafrost carbon release could be added to our model by first creating a new reservoir called PERMAFROST C and then adding a flow from it to ATMOSPHERE. The flow, which might be called melting, could be defined similarly to the soil respiration flow:
` F_(pf) = 0.05*(("PermafrostC")/(INIT("PermafrostC")))*(1+(Tsens_(pf)*DeltaT)) ` ` Tsens_(pf) = 40 `Here, the initial flow value is set to be very small, such that at the start of the model, it is insignificant. The temperature sensitivity here is very large, however, and the equation creates a flow of around 3-4 Gt C/yr with the kinds of warming we expect by the end of the 21st century.

![[creative commons]](/images/creativecommons_16.png)
Runoff
Although most of the carbon loss from the soil reservoir occurs through respiration, some carbon is transported away by water running over the soil surface. This runoff is eventually transported to the oceans by rivers. The actual magnitude of this flow is a bit uncertain, although it does appear to be quite small. The most recent estimates place it at 0.6 Gt C/yr. In our model, we will define this as a standard draining process (first-order kinetic process) as follows:
` F_r = Soil * (0.6/(INIT(Soil))) `where Fr is the runoff flow to the ocean in Gt C/yr.
All Together
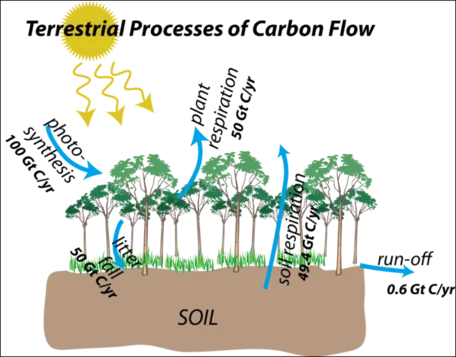
![[creative commons]](/images/creativecommons_16.png)
Figure 20 shows the terrestrial flow processes once again, but this time with the estimated magnitudes of the flows included. Most of these are very large flows, and they have a seasonality to them — photosynthesis is obviously big in the growing season, but it is small in the winter. If land masses and land plants were equally divided in the northern and southern hemispheres, this seasonality would cancel out, but in today's world, a large majority of land and plants are in the northern hemisphere, so around July, photosynthesis is very strong. As mentioned above, this on and off aspect of photosynthesis is the primary reason for the seasonal changes in atmospheric CO2 concentrations seen in the Mauna Loa record.
The Marine Carbon Cycle
Far less obvious to us than the terrestrial processes we just discussed, the cycling of carbon in the oceans is tremendously important to the global carbon cycle. For example, the oceans absorb a large portion of the CO2 emitted through anthropogenic activities. As with the terrestrial part of the global carbon cycle, we will explore here the various processes involved in transferring carbon in and out of the oceans. In Fig. 21, we see a general depiction of the flows involved in the oceanic realm, along with their magnitudes.
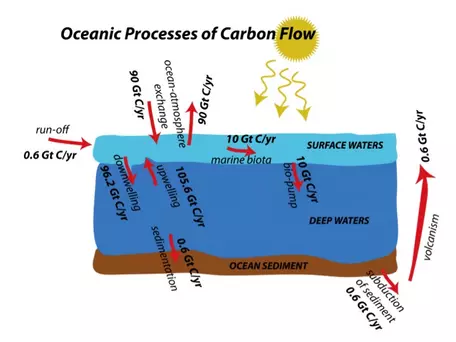
![[creative commons]](/images/creativecommons_16.png)
Ocean-Atmosphere Exchange
The exchange of gas between the air and the sea is, in theory, governed by the rate of diffusion and the distance the diffusion has to cover.
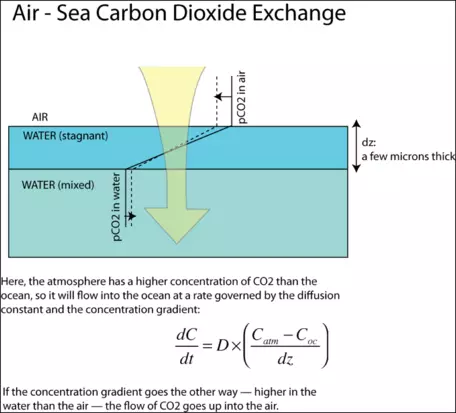
![[creative commons]](/images/creativecommons_16.png)
As depicted in Fig. 22, the concentrations in the air and the sea are relatively constant (spatially, not temporally) since these two media undergo rapid and turbulent mixing that tends to even out any systematic variations. The exception to this is a thin layer of water, just 20 to 40 microns thick, which, because of the surface tension of the water, is unable to mix well. This stagnant film is the barrier across which the diffusion of CO2 has to occur. The rate of gas transfer, or flux, is given by the equation shown in the figure. The units of the diffusion coefficient are in m2/yr and the units of the concentrations are g/m3, so the overall units of flux are in g/m2yr. When this quantity is multiplied by the surface area of the ocean, then we have the overall rate of transfer between the atmosphere and ocean in g/yr. In our model, we will represent the diffusion process in the following way (from Broecker and Peng, 1993):
` F_(ao) = k_(ao)(pCO2_(atm) - pCO2_(oc)) ` where ` F_(ao) ` is the flux of CO2 from the atmosphere to the oceans, ` pCO2_(atm) ` is the partial pressure of carbon dioxide in the atmosphere, and ` pCO2_(oc) ` is the partial pressure of carbon dioxide in the ocean water. ` k_(ao) = 0.278 ` (Gt C yr-1 ppm-1), and is a constant that combines the diffusion constant, the stagnant film thickness, and the area of the oceans. In our model, we will take `k_(ao) ` to be a constant, but it is important to consider that this parameter incorporates the stagnant film thickness, which is related to wind velocity. Higher velocity winds lead to a thinner stagnant film and thus to a faster gas transfer rate.How has this coefficient been determined? Several methods have been used, but one of the more interesting involves the use of extra 14C that was generated by atmospheric nuclear explosion tests. These tests stopped in about 1963, and since that time, the abundance of 14C in the atmosphere has steadily declined. Part of the decline is due to radioactive decay, but a major part of the decline is due to absorption by the oceans. The abundance of 14C in seawater, and its distribution with depth, are observations that provide enough information to determine the coefficient of gas transfer. This effectively amounts to using the bomb-generated 14C as a tracer in the sea — an unexpected benefit of the nuclear weapons program.
In the real world, there are important spatial variations in the gas transfer rate between the ocean and atmosphere that can be seen in Figure 23, which represents a kind of snapshot of this transfer across the globe. The units here are grams of C per m2 per year and each box is about 1e6 m2. The red, orange, and yellow colors represent places where the oceans are giving up CO2 to the atmosphere; the light blue and dark blue areas are places where the oceans are sucking up atmospheric CO2. Summing these up, we find that the oceans are taking up around 92 Gt C/yr and are releasing about 90 Gt C/yr — for a net flow of 2 Gt C/yr into the oceans. This exchange is variable in space and time, but a few general patterns can be pointed out. In general, the colder parts of the oceans absorb CO2and the warmer parts release CO2into the atmosphere. This makes sense because CO2is more soluble in cold water than in warm water.
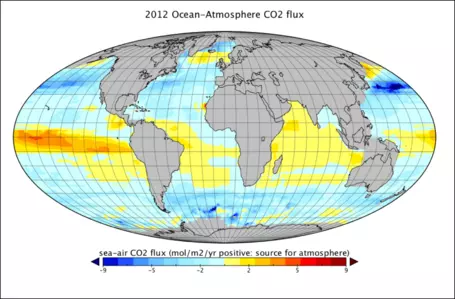
![[creative commons]](/images/creativecommons_16.png)
Carbonate Chemistry of Seawater
A series of chemical reactions occur when CO2 is absorbed by seawater, and these reactions have important consequences for the ocean's ability to absorb extra CO2from the atmosphere, and for the acidity of the oceans, which is important for the oceanic biota. When CO2 enters seawater, it reacts with water and forms a series of products, as described in the following equation:
CO2 + H2O <--> H2CO3 <--> H+ + HCO31- <--> 2H+ + CO32-
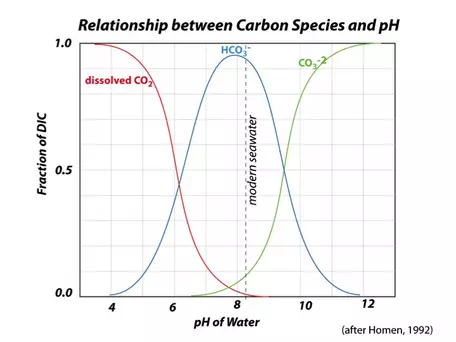
(This equation, and those following — eqns. 1-11 — are from Walker (1991), but are also included in Broecker and Peng, (1993). This means that in seawater, you can find all of these different forms (called "species") of carbon co-existing, but in reality, bicarbonate (HCO3-) is the dominant form of inorganic carbon; carbonate (CO32-) and dissolved CO2 are important, but secondary (Fig. 24). In order for our model to accurately reflect the ocean-atmosphere exchange of carbon, we need to be able to calculate the concentration of dissolved CO2 in the surface oceans, and to do that, we have to wade into some details of these chemical reactions; doing so also will allow us to calculate the pH of the surface oceans, which is critically important to the oceanic biota.
![[creative commons]](/images/creativecommons_16.png)
In the above equation, the double-headed arrows mean that the reactions can go in both directions and generally do until some balance of the different compounds is achieved — a chemical equilibrium. Each of these reactions has associated with it an equilibrium constant, which establishes the relative concentrations of the compounds on either side of the reaction. For instance, if we isolate two of the above reactions,
H2CO3 --> H+ + HCO3-
and
HCO3- --> H+ + CO32-
we can say that the equilibrium constants, k1 and k2, are given by a ratio formed by the concentrations of the various compounds involved:
` k_1 = ([H][HCO_3])/([H_2CO_3]), k_2 = ([H][CO_3])/([HCO_3]) ` Eqn. 1We can do some algebra with these equations, just like normal equations. Our goal is to find an expression for the concentration of H2CO3, which will enable us to calculate the dissolved CO2, so we begin by rearranging the equation on the left above to the following form:
` [H_2CO_3] = ([H][HCO_3])/k_1 ` Eqn. 2Then we rearrange the equation on the right so that it becomes: ` [H] = (k_2[HCO_3])/([CO_3]) ` Eqn. 3
If we know or calculate the concentration (or activity) of hydrogen — [H] — it is an easy step to get the pH of the seawater, by taking the negative log of [H], which our model can keep track of. Next, we substitute (3) into (2), to give us our desired equation expressing H2CO3 in terms of HCO3- and CO32-.
` [H_2CO_3] = k_2/k_1([HCO_3]^2/([CO_3])) ` Eqn. 4Ultimately, we want an expression for the concentration of CO2 gas contained in seawater; this is usually expressed as the partial pressure of CO2, with units of `muatm ` (micro-atmospheres), or ppm (parts per million, by volume) rather than a typical concentration, which would have units of moles per cubic meter of water. The partial pressure is given by the following formula: ` pCO_2 = K_3[H_2CO_3] ` Eqn. 5
in which K3 is a slightly different kind of equilibrium constant that incorporates the solubility of CO2 in seawater, which is a function of temperature and salinity. Our next step is to combine the various equilibrium constants into a single value as:
` KCO_2 = K_3(k_2/k_1) ` Eqn. 6keeping in mind that this value will be a function of temperature and salinity. Then we can substitute (4) and (6) into (5) to obtain another expression for the partial pressure of carbon dioxide gas in seawater:
` pCO_2 = KCO_2([HCO_3]^2/([CO_3])) ` Eqn. 7The next thing we need to do is to find expressions for the concentrations of carbonate and bicarbonate in terms of the total amount of carbon dissolved in seawater, which will change over time as the oceans release or absorb CO2 from the atmosphere. First, we need to define a term for the total concentration of inorganic carbon in solution — the DIC (dissolved inorganic carbon), or ` sum CO_2 `: ` sum CO_2 = [HCO_3] + [CO_3] ` Eqn. 8
This is an approximation since it ignores CO2 gas and H2CO3, but both of these are very minor components of the total carbon in the oceans. This sum, the concentration of total dissolved carbon, is simply equal to the amount of carbon in the ocean reservoir divided by the volume of the ocean. Looking at equation 8, we see that it does not tell us the relative proportions of the carbonate and bicarbonate — just their combined concentration. So, we need to find some other means of establishing the proportions of these two forms of carbon.
We get some help from the fact that the relative proportions of bicarbonate (HCO3-) and carbonate (CO32-) play an important role in establishing the balance of positive and negative charges in seawater, as shown in the table below (data from Broecker and Peng, 1993). Charge balance must be maintained, otherwise the oceans would probably explode (but this cannot really happen because chemical reactions would quickly take place to bring about the charge balance).
Table 1: Charge Balance in the Oceans
| Cation | mmoles/kg | mEq/kg | Anion | mmoles/kg | mEq/kg |
|---|---|---|---|---|---|
| Na+ | 470 | 470 | Cl- | 547 | 547 |
| K+ | 10 | 10 | SO42- | 28 | 56 |
| Mg2+ | 53 | 106 | Br- | 1 | 1 |
| Ca2+ | 10 | 20 | Sub-total --- | 604 | |
| Total+ | 606 | HCO3 + CO3 | 2 | ||
| Total --- | 606 |
Cations like calcium (Ca2+), sodium (Na+), potassium (K+), and magnesium (Mg2+) all add positive charges to seawater; these are partially countered by the main anions, chloride (Cl-), sulfate (SO42-), and bromide (Br-), but the result is a slight deficit of negatively charged ions. This difference is essentially made up by the carbonate and bicarbonate ions. If more negative charge is needed, then more of the carbon occurs in the form of carbonate since it has a charge of minus 2, while if less negative charge is needed, more of the carbon exists in the form of bicarbonate.
The excess positive charge of seawater that needs to be balanced by the different forms of dissolved carbon is called the alkalinity of the seawater (a value of 2 in the table above). The alkalinity is defined as:
` Alk = [HCO_3] + 2[CO_3] ` Eqn. 9Note that the carbonate ion counts twice since it has a minus 2 charge. It is important to realize that the total alkalinity is really determined by the other ions in solution — the ones mentioned above. Looking at the above equation, you can see that with a given alkalinity, if we have just a little dissolved carbon, more of the carbon will be in the form of the carbonate ion (CO32-) in order to make up the charge imbalance, but if we have a high concentration of dissolved carbon, there will be a greater proportion of the bicarbonate ion (HCO3-). The concentrations of both the carbonate and bicarbonate ions can be expressed as a function of both the alkalinity and the concentration of total dissolved inorganic carbon, ` sum CO_2 `, as shown in the following:
` [CO_3] = Alk - sum CO_2 ` ` [HCO_3] = 2 sum CO_2 - Alk ` Eqn. 10
Here, we need to remember that this is an approximation because we ignored the term for H2CO3 in Equation 8. In the model we will eventually experiment with, we use a more precise formulation that does not ignore the concentration of H2CO3. This increases the complexity of the algebra, giving us a quadratic equation whose solution ends up as:
` [HCO_3] = (sum CO_2 - sqrt(sum CO_2^2 - Alk(2 sum CO_2 - Alk)*(1 - 4k_2/(k_1))))/((1 - 4k_2/(k_1))) ` ` [CO_3] = ((Alk - [HCO_3])/2) ` Eqn. 11Regardless of whether we consider the more digestible form (10) or the more precise form of expressing HCO3- and CO32- (11), we are finally set, because if we look at the equation for the partial pressure of CO2--
` pCO_2 = KCO_2 *([HCO_3]^2/([CO_3])) ` Eqn. 7-- we see that all of the terms can be expressed in terms of components of the model. We have reached the light at the end of the algebraic tunnel.
As can be seen, the chemistry of carbon in seawater is relatively complex, but it turns out to be extremely important in governing the way the global carbon cycle operates and explains why the ocean can swallow up a good deal of the atmospheric CO2 without having its own CO2 concentration rise very much. In our STELLA model, all of the equilibrium constants (and their sensitivities to temperature), the alkalinities, the concentrations of the different carbon species, and the pH are calculated at each time step to arrive at a pCO2 that then governs the rate of exchange with the atmosphere.
Summary of Carbonate Chemistry
Let us see if we can summarize this carbonate chemistry — it is important to have a good grasp of this if we are to understand how the global carbon cycle works.
- Carbon can exist in three main inorganic forms in seawater — CO2, HCO3-, and CO32-, and there is a rapidly-achieved equilibrium between these species.
- The ratio of HCO3- to CO32- along with the water temperature determines the CO2concentration of seawater and also the pH.
- The temperature of the water also controls how much CO2 occurs in the form of dissolved gas, thus affecting the concentration of CO2 gas in seawater.
- The alkalinity of seawater represents the positively-charged ions that need to be countered by negatively-charged carbonate and bicarbonate ions.
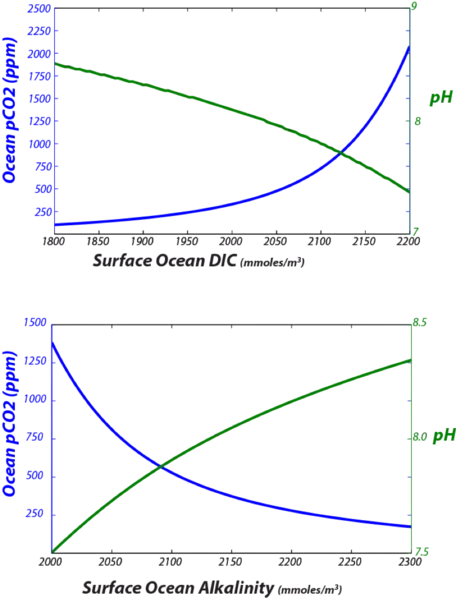
- The concentration of the total dissolved inorganic carbon (DIC), along with the alkalinity, determines the ratio of HCO3- to CO32-(see Eqn. 10 above), and thus the CO2 concentration of seawater (Eqn. 7 above). If we increase DIC without changing the alkalinity, then more carbon must be in the form of HCO3-, which decreases the pH (the negative log of [H] from Eqn. 3 above) and increases the dissolved CO2 concentration of seawater.
- The CO2 concentration of seawater, relative to the atmospheric CO2, determines whether the oceans absorb or release CO2. Currently the cold parts of the oceans absorb atmospheric CO2 and the warm regions of the oceans release CO2 to the atmosphere.
- The ability of carbon to switch back and forth between these three forms means that only a portion of the CO2 absorbed by the oceans will remain as CO2.
Some of the key relationships are illustrated in the graphs in Fig. 25.
![[creative commons]](/images/creativecommons_16.png)
Marine Biota Exchange — The Biologic Pump
The surface waters of the world's oceans are home to a great number of organisms that include photosynthesizing phytoplankton at the base of the food chain. These plants (and cyanobacteria) utilize CO2 gas dissolved in seawater and turn it into organic matter, and just like land plants, these phytoplankton also respire, returning CO2 to the surface waters. The net transfer, ` F_(ob) `, is defined in our model as follows:` F_(ob) = 10(("OceanBiota")/(INIT("OceanBiota"))) `
where OceanBiota has a starting value of 3 Gt of carbon (see figure 1), and 10 is the flux of carbon between the biota and surface waters when the carbon cycle is in a steady state.
At the same time as phytoplankton are turning CO2 into organic matter, many planktonic organisms extract dissolved carbonate ions from seawater and turn them into CaCO3 (calcium carbonate) shells (Fig. 26). When these planktonic organisms die, their soft parts are mainly consumed and decomposed very quickly, before they can settle out into the deeper waters of the oceans. This decomposition thus returns carbon, in the form of CO2, to seawater.

![[creative commons]](/images/creativecommons_16.png)
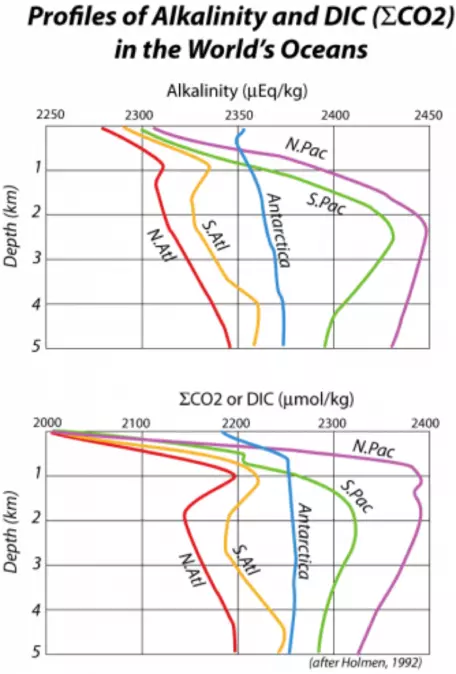
However, a small portion of the organic remains and the inorganic calcium carbonate shells sink down into the deep oceans, thus transferring carbon from the shallow surface waters into the huge reservoir of the deep oceans. This transfer is often referred to as the biologic pump, and it causes the concentration of CO2 gas, and also of DIC in the surface waters, to be less than that of the deeper waters. This can be seen in Fig. 27, which shows the vertical distribution of DIC (and also alkalinity) in a profile view for some of the major regions of the world's oceans.
![[creative commons]](/images/creativecommons_16.png)
Why is the alkalinity reduced in the surface waters? For the same reason that DIC is depleted. Planktonic organisms make shells of CaCO3, and when these sink to the seafloor, they carry Ca2+ ions with them, thus reducing the alkalinity of the surface waters. Much of this CaCO3 is later dissolved when it reaches deeper parts of the oceans, which explains the higher alkalinity values in the deep waters (Fig. 27). By controlling the concentration of CO2 gas dissolved in the surface waters, the planktonic organisms exert a strong influence on the concentration of CO2 in the atmosphere. For instance, if the biologic pump were turned off, atmospheric CO2 would rise to about 500 ppm (compared to the current 400 ppm); if the pump were operating at maximum strength (i.e., complete utilization of nutrients such as phosphorus, nitrogen, and potassium), atmospheric CO2 would drop to a low of 140 ppm. Clearly, this biologic pump is an important process. In our model, the pump is defined as follows:
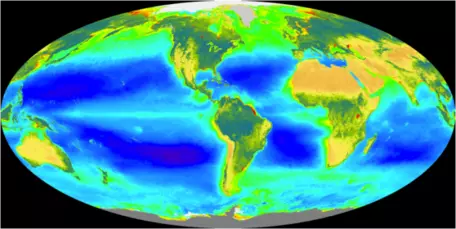
` F_(bp) = 10(("OceanBiota")/(INIT("OceanBiota"))) `What controls the strength of this biologic pump? The photosynthesizing plankton require nutrients in addition to CO2 in order to thrive; specifically, they require nitrogen and phosphorus. Most of these plants need P, N, and C in a ratio of 1:16:125, and since at present the ratio of P to N in ocean water is about 1:16, both P and N limit the growth of these phytoplankton. Photosynthetic activity of plankton can be mapped out by satellites tuned to record differences in water color due to the presence of chlorophyll. This distribution is shown in Fig. 28.
![[reuse info]](/images/information_16.png)
If the nutrients in seawater were being utilized to the maximum extent possible, there would be practically no P or N dissolved in seawater. But in fact, the concentration of P tells us that the biologic pump is not operating at maximum efficiency. In the map shown in Figure 29, the purple areas represent regions with no phosphate in the surface water of the oceans, meaning that there is simply a lack of nutrients, or that all the nutrients are utilized. In particular, it is the cold, polar regions that are not utilizing all of the available nutrients. This may be due in part to the temperature, but it may also be related to a paucity of iron, a minor nutrient that is apparently lacking in the colder regions, especially in the Southern Ocean, ringing Antarctica.
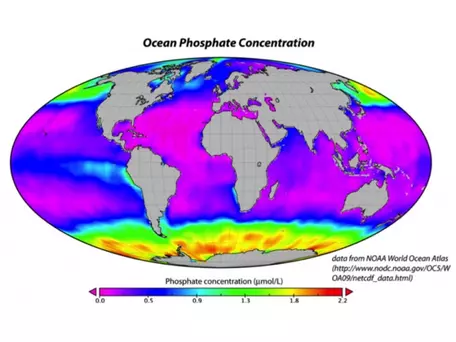
![[creative commons]](/images/creativecommons_16.png)
In addition to nutrients, the strength of the biological pump is sensitive to the pH of the ocean water. The organisms in the oceans are adapted to a pH of around 8.3 or 8.4, but if the oceans take up too much CO2 too quickly, the pH will decrease and move outside the optimum range for these organisms. Thus, lower pH levels (i.e., higher acidity) will probably mean a reduction in the strength of the biological pump, which will in turn limit the oceans' ability to absorb more carbon.
Downwelling
Downwelling (sinking of dense water) transfers cold and/or salty surface waters into the deep interior of the oceans, and as a result, carbon is transferred as well. The magnitude of the flow is thus a function of the volume of water flowing and the average concentration of carbon in the surface waters, which is itself a function of the total amount of carbon stored in the surface water reservoir — assuming that the size of the reservoir is not changing appreciably over the few hundred years that our model is intended to be used for.
Downwelling occurs primarily near the poles, where surface waters are strongly cooled by contact with overlying frigid air. This cooling leads to a density increase in the surface waters, prompting them to sink. Another cause of density increase in surface water is the formation of ice from seawater. This process is particularly active at the margins of Antarctica and increases the salinity of the seawater there as salt is expelled in the creation of ice. The dense water remaining after ice formation then sinks and flows through the deep oceans, effectively mixing them on a timescale of about 1000 years or so (the Atlantic Ocean mixes somewhat faster, which helps explain the smaller ΣCO2 and alkalinity gradients seen in Fig. 27). Although the model does not allow for a change in downwelling, it is something that is expected to change if the oceans continue to warm — e.g., melting Greenland's ice and adding that fresh water to the North Atlantic might disable the downwelling that occurs there (see Module 8 on Thermohaline Circulation).
Upwelling
Upwelling is just the opposite of downwelling, and the total transfer of carbon is a function of the volume of water involved in this flow and the amount of carbon stored in the deep ocean reservoir. Upwelling occurs in areas of the oceans where winds and surface currents diverge, moving the surface waters away from a region; in response, deep waters rise up to fill the "void." Upwelling occurs along the equator, where there is a strong divergence, and also along the margins of some continents, such as the west coast of South America. In addition to carbon, this upwelling water brings with it nutrients such as nitrogen and phosphorus, making these waters highly productive.
The amount of carbon transferred by upwelling is greater than the downwelling flow. This is not because the volume of flow is different in these two processes, but rather because the concentration of carbon in the deep waters of the ocean is greater than that in the shallow surface waters, due in part to the operation of the biologic pump mentioned above. In our model, we combine the upwelling and downwelling flows into one ocean mixing bi-flow (Fom), formulated as:
Fom = wflux * (Cd - Cs) / 8.33e13Here, wflux is the exchange of water involved in upwelling and downwelling (measured in m3 per year), Cd and Cs are the concentrations of carbon in the deep and shallow oceans (expressed in moles C per m3) and 8.33e13 converts from moles C per year to Gt C per year.
Alkalinity Exchange
As mentioned earlier, upwelling, downwelling, and the biologic pump influence the alkalinity of the surface and deep oceans. Because we need to know the surface alkalinity in order to calculate the pCO2 of the oceans, we have to keep track of the alkalinity in the two ocean reservoirs. We will do this through the use of two alkalinity reservoirs linked by two flows — one being the biologic pump and the other being the combined effects of upwelling and downwelling. The alkalinity units are in moles and the fluxes are expressed in terms of moles per year. We will call the flux related to the biologic pump carbonate_rain (Fcr), expressed as follows (after Walker, 1991):
Fcr = (Fbp * 8.33e13) * (2 * 0.25 - 0.15)
The first term in parentheses (Fbp) gives us the biologic pump flow in moles/year. The second term in parentheses reflects the fact that there are 2 moles of alkalinity per mole of carbonate, but only a quarter (0.25) of the total biologic pump flux is carbonate (the rest is organic) and then 0.15 of the biologic pump is nitrogen, which will become a negatively charged ion and thus detract from alkalinity.
The alkalinity mixing flow we'll call up_dwn (Fud) and express as follows (after Walker, 1991):
Fud = wflux * (Cad - Cas)
where wflux is as defined before and Cad and Cas are the concentration of alkalinity in the deep and surface oceans, respectively, which are obtained by dividing the total alkalinity in each reservoir by the reservoir volumes. wflux is measured in m3/yr while Cad and Cas are in moles/m3, giving us moles/yr as the final units for Fud.
Sedimentation
Some of the carbon, both organic and inorganic (i.e., calcium carbonate shells), produced by marine biota and transferred to the deep oceans settles out onto the seafloor and accumulates there, eventually forming sedimentary rocks (Fig. 30). The magnitude of this flow is small — about 0.6 Gt C/yr — relative to the total amount of carbon transferred by sinking from the surface waters — 10 Gt C/yr. The reason for this difference is primarily because the deep waters of the oceans dissolve calcium carbonate shell materials; below about 4 km, the water is so corrosive that virtually no calcium carbonate material can accumulate on the seafloor. In addition, some of the organic carbon is consumed by organisms living in the deep waters and within the sedimentary material lining the seafloor. This consumption results in the release of CO2 into the bottom waters and thus decreases the amount of carbon that is removed from the ocean through sedimentation. It is worth noting that the process of organic carbon consumption on the seafloor is another microbial process and is very similar to the soil respiration flow described earlier. Since the microbes living on the seafloor require oxygen to efficiently accomplish this task, the supply of oxygen to the seafloor by deep currents is an important part of this process. In our model, we will express this sedimentation flow (Fs) as a fraction of the carbon exported to the deep ocean via the biologic pump:
` F_s = 0.6*(F_(bp)/10) `where Fbp is the biologic pump flow and 10 is its initial value; the units are in Gt C/yr.

![[creative commons]](/images/creativecommons_16.png)
Volcanism and Metamorphism
When sedimentary rocks deposited on oceanic crust are subducted at a trench where two tectonic plates of Earth's surface converge, they may melt or undergo metamorphism; in either case, the carbon stored in calcium carbonate — limestone — is liberated in the form of CO2, which ultimately is released at the surface. The CO2 may come out when a volcano erupts, or it may slowly diffuse out from Earth's interior via hot springs, but in both cases, these processes represent a transfer of carbon from the reservoir of sedimentary rocks to the atmosphere. The magnitude of this flow is quite small, and is adjusted here to a value of 0.6 Gt C/yr in order to allow the model to exhibit a steady state. This flow is defined as a constant in the model, although in reality, it varies according to the timing of large volcanic eruptions. An extremely large volcanic eruption may emit carbon at a rate of around 0.2 Gt C/yr for a year or two, creating a minor fluctuation.
Human Influences on the Global Carbon Cycle
Fossil Fuel Burning
Another pathway for carbon to move from the sedimentary rock reservoir to the atmosphere is through the burning of fossil fuels by humans (Fig. 31). Fossil fuels include petroleum, natural gas, and coal, all of which are produced by slow transformation of organic carbon deposited in sedimentary rocks — essentially the fossilized remains of marine and land plants. In general, this transformation takes many millions of years; most of the oil and gas we now extract from sedimentary rocks is on the order of 70–100 million years old. New fosssil fuels take a very long time to form, and we are using them up much much faster than they are being formed, meaning that if we keep using fossil fuels at the rate we are today, we will run out! The run-out date depends on new discoveries and our ability to extract fuels more efficiently by processes like fracking, but we will be close to running out by the end of this century unless we figure out a way to tap into the huge reserves of gas hydrates trapped in oceanic sediments.

![[creative commons]](/images/creativecommons_16.png)
Fossil fuels are composed primarily of carbon and hydrogen. For instance, methane, the main component of natural gas, has a chemical formula of CH4; petroleum is a more complex compound, but it too involves carbon and hydrogen (along with nitrogen, sulfur and other impurities). The combustion of fossils fuels involves the use of oxygen and the release of carbon dioxide and water, as represented by the following description of burning natural gas:
CH4 + 2O2 => CO2 + 2H2O
Beginning with the onset of the industrial revolution at the end of the 19th century, humans have been burning increasing quantities of fossil fuels as our primary energy source. As a consequence, the amount of CO2 emitted has undergone an exponential rise that has followed the exponential rise in the human population. The magnitude of this flow is currently about 9 Gt C/yr. This number also includes the CO2 generated in the production of cement, where limestone is burned, which liberates CO2.
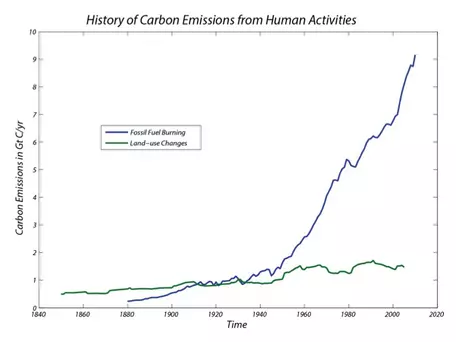
![[creative commons]](/images/creativecommons_16.png)
As you can see (Fig. 32), the flow of carbon associated with human emissions has changed considerably over time as our population has increased and as our economies have become more industrialized with a big thirst for the energy provided from combustion of fossil fuels. The model we will work with in the lab activity for this module includes this history of emissions, beginning in 1880 and going up to 2010; beyond 2010 is the realm of future projections, which can be altered to explore the consequences of choices we might make or not make in the future.
Land-Use Changes — Forest Burning and Soil Disruption
Another form of human alteration of the global carbon cycle is through forest cutting and burning and the disruption of soils associated with agriculture. When deforestation occurs, most of the plant matter is either left to decompose on the ground or is burned, the latter being the more common occurrence. This process reduces the size (the mass) of the land biota reservoir, and the burning adds carbon to the atmosphere. Land-use changes other than deforestation can also add carbon to the atmosphere. Agriculture, for instance, involves tilling the soil, which leads to very rapid decomposition and oxidation of soil organic matter. This means that in terms of our model, we are talking about two separate flows — one draining the land biota reservoir, the other draining the soil reservoir; both flows transfer carbon to the atmosphere. Current estimates place the total addition to the atmosphere from forest burning and soil disruption at around 1-2 Gt C/yr (Fig. 32); estimates divide this into 70% to 50% forest burning, with soil disruption making up the remainder.
Readings and Key References
Broecker, W.S., and Peng, H.-S., 1993, Greenhouse Puzzles, New York, Eldigio Press, 251 p.
Gifford, R.M., 1993, "Implications of CO2 effects on vegetation for the global carbon budget," in Heimann, M., (ed.), The Global Carbon Cycle, NATO ASI Series, v. 115, p. 159–200.
Holmen, K., 1992, "The Global Carbon Cycle," in Butcher, S., Charlson, R., Orians, G., and Wolfe, G., (eds.), Global Biogeochemical Cycles, London, Academic Press, p. 237–262.
IPCC, 1995, Climate Change 1994, Cambridge, Cambridge University Press, 339 p.
Kump, L., 1991, "Interpreting carbon-isotope excursions: Strangelove oceans," Geology, v. 299, 302.
Kump, L., Kasting, J., and Crane, R., 2010, The Earth System, 3rd Edition, Pearson, 420 p.
Kwon, O.-Y., and Schnoor, J.L., 1994, "Simple global carbon model: the atmosphere-terrestrial biosphere - ocean interaction," Global Biogeochemical Cycles, v. 8, p. 295-305.
Marland, G., Boden, T.A., and Andres, R.J., 2003. "Global, Regional, and National CO2 Emissions." In Trends: A Compendium of Data on Global Change. Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy, Oak Ridge, Tenn., U.S.A.
Post, W.M., Peng, H.-S., Emanuel, W.R., King, A.W., Dale, V.H., and DeAngelis, D.L., 1990, "The global carbon cycle," American Scientist, v. 78, p. 310–326.
Siegenthaler, U., and Sarmiento, J.L., 1993, "Atmospheric carbon dioxide and the ocean," Nature, v. 365, p. 119–125.
Walker, J.C.G., 1991, Numerical Adventures with Geochemical Cycles, Oxford, Oxford University Press, 192 p.

































