Unit 2 Reading: Growth and Dynamics of Populations

by Kirsten Menking, Vassar College

In this week's modeling project, we explore the factors that lead populations of organisms to grow or decline over time and contemplate whether current rates of human population growth are sustainable.

Introduction

In 1995, population scientist Joel E. Cohen at the Rockefeller University published a book titled How Many People Can the Earth Support? At the time, Earth's human population measured 5.7 billion, a number that some scientists thought exceeded, by several billion, the value the planet could support indefinitely. Others were more optimistic, suggesting 12–14 billion as a limiting value. One particularly outlandish estimate came in at one trillion, though the greatest frequency of opinions ranged between 7.7 and 12 billion (Cohen, 1995). Those with a pessimistic outlook pointed to dwindling amounts of arable land needed to feed burgeoning populations, per capita decreases in freshwater availability, unsustainable agricultural practices that lead to soil erosion and mining of groundwater, and accumulation of pollution associated with industrialized societies. Optimists called on technological advances in agriculture to supply future populations with the food they will need to survive as well as better accounting of water use to reduce instances of waste, an increased frequency of recycling, and reduction of hazardous chemical use.

Some 20 years after Dr. Cohen's book was published, Earth's human population has grown to ~7.25 billion. To date, the mass starvation predicted by resource pessimists has not occurred, though there are pockets of famine, and the United Nations World Food Program estimates that 805 million people are malnourished (http://www.wfp.org/hunger/stats; Fig. 1). At the same time, it is clear that a tremendous amount of food is wasted, such that food insecurity may be more a result of sociopolitical factors than related to global environmental constraints. Still, the lack of widespread starvation does not necessarily mean that Earth is capable of sustaining its current human population indefinitely, and Dr. Cohen noted in 1995 and in subsequent work (see, for example, http://www.nytimes.com/2011/10/24/opinion/seven-billion.html?pagewanted=all&_r=0) that it is quite difficult to answer the question that forms the title of his book. In large measure this difficulty stems from the fact that the future is inherently unknowable, but to be more concrete, it is hard to predict human behavioral changes that could lead to either a better or a worse outcome for our species. In addition, while scientific progress and knowledge of the natural world have exploded in the last few decades, we continue to have only limited understanding of the complex and interconnected ecological processes that make our planet such a favorable environment. It is possible that continued growth of the human population will stress some ecological systems to the point of collapse, with unknown consequences for us. Habitat fragmentation as a result of human agriculture and settlement, bioaccumulation of human-made toxins, introduction of exotic invasive species by human travel and trade, and human-induced climate change are presently contributing to what some have identified as the sixth mass extinction event in Earth's history (Kolbert, 2014; Merritts et al., 2014). Previous mass extinctions, whether caused by meteorite impacts or other factors, led to massive biosphere changes that allowed the evolution and/or rise of new classes of organisms (Barnosky et al., 2012). For example, the bolide that struck the Yucatan Peninsula 65 million years ago killed off the dinosaurs and ushered in the age of mammals.

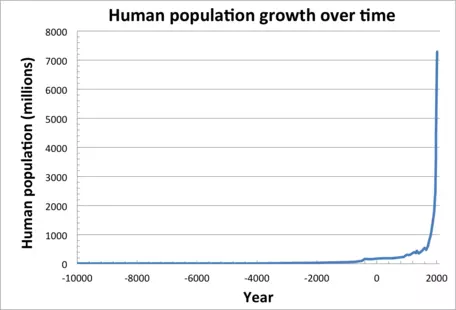
While the future is difficult to predict, some things are clear: the human population and its environmental impact are presently larger than they ever have been in Earth history, and human population growth has followed a nearly exponential increase over the past few centuries (Fig. 2). Homo sapiens is about 200,000 years old, and it took all of human history up to the early 1800s A.D. for our population to climb to 1 billion. Since that time, we have increased rapidly, and it presently takes about 13 years for our population to increase by another billion people. Inasmuch as the Earth and its resources are not expanding, it is clear that the path we are on cannot continue forever. It is also clear that we have much to gain from studying the population growth of other species and what factors keep their numbers in check.

Trophic Levels and Food Webs

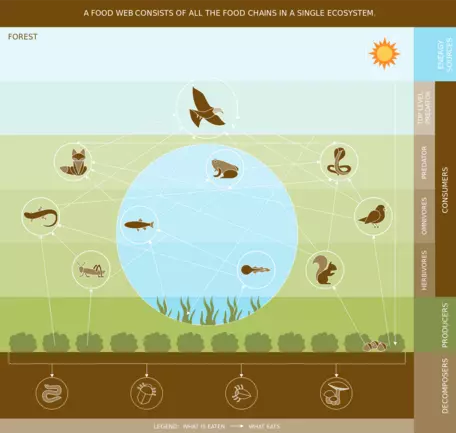
Organisms on Earth are connected to one another through complex food webs that facilitate the movement of matter and energy throughout the biosphere (Fig. 3). These food webs are made up of overlapping food chains defined by feeding relationships (Ricklefs, 2008).

At the base of food chains, plants capture and store solar energy through the process of photosynthesis, converting that energy into carbohydrates, proteins, and fats in association with nutrients found in soils such as carbon, nitrogen, and phosphorus. Plants, in turn, are consumed by herbivores, which may themselves be consumed by omnivores or carnivores. While nutrients and energy move upward through the food chain via these relationships, they may also move back down into the soil through the activities of decomposer organisms that have evolved to feed on the waste products and corpses of other organisms. One organism's waste is another organism's food, a relationship that ensures perpetual recycling and redistribution of essential nutrients throughout the biosphere.

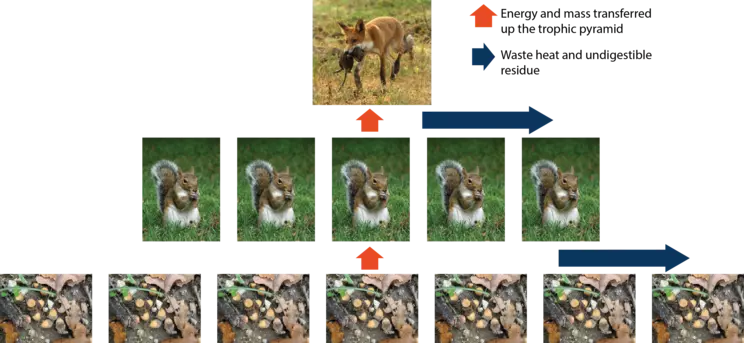
Not every part of an organism winds up being edible to the creatures that feed on it. Substantial amounts of energy go into producing woody material, bones, shells, fur, and claws, but these materials are rarely digestible to consumers. In addition, much of the food energy that an animal takes in is used for metabolic processes that result in the production of heat that flows from the animal into the surrounding environment. As a result, large amounts of energy are lost at each level of the food chain, and the number of individuals capable of being supported likewise declines up the chain (Kaufmann and Cleveland, 2008). For example, a squirrel may need to consume thousands of acorns to survive throughout the year (Fig. 4). A fox, on the other hand, may require dozens of squirrels or other small mammals to get through a year. The loss of energy up the food chain means that the number of foxes that can be supported is always much smaller than the number of squirrels, which in turn is smaller than the number of acorns. At this point, it is worth contemplating the position of humans within the food chain and the size of our population. Given our numbers, do you think that our species is in ecological balance?

Population Controls

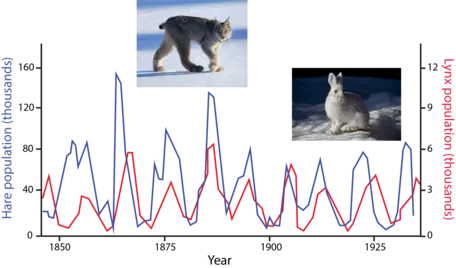
In general, populations of organisms cannot grow exponentially for long before they either run out of food or produce so much waste that they render their environment unlivable. German chemist Justus von Liebig (1803-1873) was the first person to realize that all organisms are limited by some substance (typically nitrogen or phosphorus) in short supply (Merritts et al., 2014), and he conceived of the first chemical fertilizers as a means of increasing plant productivity. Liebig's "Law of the Minimum" states that the growth of organisms depends on the availability of the scarcest resource they require and helps to explain one of the most fascinating population cycles ever discovered involving Canada lynx and snowshoe hares (Fig. 5).

For several decades in the late 1800s and early 1900s, the Hudson's Bay Company kept track of the numbers of pelts it bought from fur trappers in Canada. British zoologist Charles Elton analyzed the company's records and noticed that populations of Canada lynx and snowshoe hares cycled between higher and lower values, with populations of lynx cresting one to two years after peaks in the population of hares (Ricklefs, 2008). The "predator-prey cycle" Elton identified starts with an increase in the number of hares. As this prey species becomes more numerous, there is more food around for the lynx to eat, allowing their population to rise. As lynx increase in number, however, the higher level of predation causes the hare population to again decline. Cut off from their food supply, the lynx begin to starve, reducing the predatory pressure on the hares, which can multiply once again. The dependency of each organism on the feeding and reproductive behavior of the other leads to a stable oscillation in numbers that prevents either from reproducing exponentially.

The limited amount of resources available for any particular organism generally leads to a limit in the number of individuals a particular environment can support (Fig. 6). This so-called "carrying capacity" can also arise from the ability of the environment to assimilate an organism's wastes (Kaufman and Cleveland, 2008). Consider, for example, a pond full of aquatic turtles. In addition to the limits imposed on the turtle population by the amount of food contained within the pond, each turtle requires a minimum volume of water containing decomposer organisms to process its waste products and render them nontoxic.

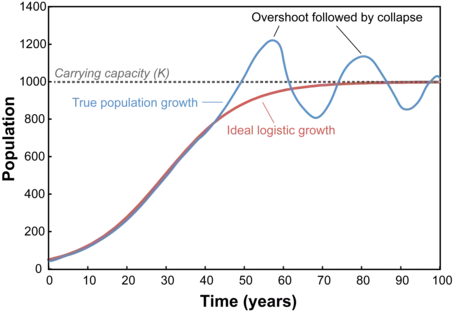
While it would be advantageous for organisms to adjust their populations to gradually approach the carrying capacity of their environments, in practice, population growth often continues beyond what the environment can sustainably support. The resulting "overshoot" of population leads to steep declines when organisms are no longer able to acquire the resources they need. If the population size falls below the carrying capacity limit, it may rebound only to experience subsequent overshoots and crashes. It remains to be seen whether Earth's human population has exceeded the carrying capacity for the planet as a whole, but there are examples throughout human history of societies that have exceeded the capability of their local environments to support them. The downfall of the Mayan culture of Central America, for example, is attributed in part to agricultural practices that led to soil erosion and desertification (Turner and Sabloff, 2012; Cook et al., 2012).

Easter Island

One of the most-often-cited examples of human-induced socio-environmental collapse is the Easter Island culture that thrived several hundred years ago on a small island in the South Pacific (Fig. 8). Colonized by Polynesians perhaps as early as 400 A.D., the island, also known as Rapa Nui, was originally covered by coconut palm forests. Several centuries later, the island was nearly totally deforested and a thriving human culture was in decline (Mieth and Bork, 2005). Easter Island is best known for its massive stone statues (Fig. 9), called moai, carved by the Polynesian immigrants who today go by the name Rapanui.

The statues are thought to have had religious significance and may have been carved to represent Rapanui ancestors. At the height of the culture, the island is estimated by several anthropologists to have had around 15,000 inhabitants. By the time Europeans visited in 1722, the population had declined to around 2000 to 3000. After first contact, the introduction of European diseases, such as smallpox and syphilis, as well as the capture of many Rapanui to be sold into the slave trade, led the population to decline further to just over 100 individuals by the late 1800s.

The cause of the pre-European population decline has captured the imagination of anthropologists for decades and was originally attributed to the agricultural practices of the Rapanui themselves (Diamond, 2005). Prior to the last decade, the generally accepted explanation for the decline of the Easter Island civilization was that the Rapanui used slash and burn or slash and rot practices to clear land for agriculture. As the population grew, more and more land was cleared, leading to soil erosion, declining soil fertility, and reduced crop yields that could no longer support the large population (Mieth and Bork, 2005). Furthermore, the loss of trees led to an end to fishing as there was no longer any wood with which to build canoes. The population overshoot thus led to environmental degradation that in turn led to societal collapse.

Recent studies have called elements of this model into question, pointing out that there is little evidence for a population as large as 15,000 at the peak and attributing much of the deforestation activity to Polynesian rats imported to the island—whether intentionally or as stowaways on canoes—by the original Rapanui settlers (Hunt, 2006). Without predators and with very high birth rates, the rat population likely increased at an exponential rate from a few breeding pairs at settlement to millions just a few years later. Archeological evidence shows that the rats foraged on the roots and coconut fruits of the palms, both killing the existing trees and preventing forest regeneration. At the same time, the Rapanui incorporated increasing amounts of rat meat into their diets, offsetting the loss of fish protein that came about from the inability to build canoes. Rather than being criticized for their poor stewardship of the land, this model suggests that the Rapanui should be celebrated for their abilities to adapt to changing environmental circumstances.

Whatever the primary cause of Easter Island deforestation, it is clear that humans played a major role and that the island lost many native flora and fauna as a result. Whether or not the human population experienced a precipitous decline, the ecosystem as a whole was decidedly degraded by the time of European arrival, a situation that may eventually have led to decline even in the absence of contact with the rest of the world.

The Mathematics of Population Growth

In the STELLA models that we create today, we will explore a variety of population growth scenarios from basic exponential growth, to logistic growth, to more complex predator-prey interactions. We will also create a model of the classical explanation of Easter Island deforestation to simulate population overshoot followed by collapse. To do so will require a bit of math. The most basic equation governing population growth states that the rate of change in the population over time ` (dN)/dt` depends on how many individuals exist at any given time (N) and the net growth rate (`lambda`, e.g. how many offspring are produced per breeding pair of adults minus the rate at which individuals die as a fraction of the total population):

` (dN)/dt=lambda N `

The analytical solution to this differential equation involves the following steps. First, we rearrange the equation so that both population terms are on the same side:

` (dN)/N=lambda dt`

Using calculus, we next integrate both sides of the equation:

`int (dN)/N=int lambda dt`

This integration results in:

`ln(N)=lambda t + c`, where t is time and c is a constant of integration.

We now get rid of the logarithm by using the exponential function on both sides of the equation:

`e^ln(N)=e^(lambda t + c)`

The exponential function (e) taken to the power of the natural logarithm of the population (ln(N)) returns the population as the result:

`N=e^(lambda t + c)`

If we think about this equation carefully, we note that N varies with t, so we should really express N as N(t):

`N(t)=e^(lambda t + c)`

Using the rules of exponents, we can restate the equation as:

`N(t)=e^(lambda t) * e^c` If we now let `C=e^c` then `N(t)=Ce^(lambda t)`

Our last task is to determine a value for C. We know that at time = 0, the initial number of parents is N₀. If we substitute these values into the equation above, we get:

`N_0=Ce^(lambda*0)` Since `e^0=1, C=N_0`

and the final analytical solution is:

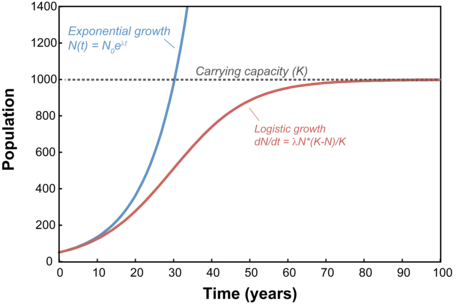
`N(t)=N_0*e^(lambda t)`

The graph of this solution is shown in Fig. 6, and as you can see there, this equation describes a population that is undergoing exponential growth. As we mentioned earlier in the reading, such growth can never be sustained indefinitely because the population will either run out of resources or create so much waste that it toxifies its environment. We also noted that such limits to growth may cause a population to achieve a stable value after some initial period of exponential growth, reflecting the carrying capacity of the environment. We can incorporate this carrying capacity (K) in the following way:

` (dN)/dt=lambda N*((K-N)/K) `

Let us look at this equation carefully. When the population (N) is very small, the ` ((K-N)/K) ` term is roughly equivalent to ` ((K-0)/K) `, which equals 1. With this tiny population, the equation becomes essentially identical to the previous exponential growth equation, and the population grows rapidly, without constraint. As the population approaches the carrying capacity, however, N becomes very close to K such that the ` ((K-N)/K) ` term of the equation effectively becomes ` ((K-K)/K) ` which equals 0. Since 0*anything = 0, ` (dN)/dt` becomes 0 and the population stops growing. The leveling off of the population leads to the characteristic S-shape of the population curve, a kind of growth known as "logistic."

References

Barnosky, A.D., Matzke, N., Tomiya, S., Wogan, G.O.U., Swartz, B., Quental, T.B., Marshall, C., et al., 2011, "Has the Earth's Sixth Mass Extinction Already Arrived?" Nature, v. 471, p. 51–57.

Cohen, J.E., 1995, How Many People Can the Earth Support? New York: W.W. Norton & Company, 532 p.

Cook, B.I., Anchukaitis, K.J., Kaplan, J.O., Puma, M.J.,, Kelley, M., and Gueyffier, D., 2012, "Pre-Columbian deforestation as an amplifier of drought in Mesoamerica," Geophysical Research Letters, v. 39, n. 16, article n. L16706.

Diamond, J., 2005, Collapse: How Societies Choose to Fail or Succeed, New York: Viking Press, 575 p.

Hunt, T., 2006, "Rethinking the fall of Easter Island," American Scientist, September-October issue.

Kaufmann, R.K., and Cleveland, C.J., 2008, Environmental Science. Boston: McGraw Hill Higher Education, Chp. 5.

Kolbert, E., 2014, The Sixth Extinction: An Unnatural History, New York: Henry Holt & Company.

Merritts, D.J., Menking, K.M., and DeWet, A.P., 2014, Environmental Geology: An Earth System Science Approach, 2nd Edition. New York: W.H. Freeman, Chp. 7.

Mieth, A., and Bork, H.-R., 2005, "History, origin and extent of soil erosion on Easter Island (Rapa Nui)," Catena, v. 63, p. 244–260.

Ricklefs, R.E., 2008, The Economy of Nature, 6th Edition. New York: W.H. Freeman, Chp. 15, 18.

Turner, B.L., II, and Sabloff, J.A., 2012, "Classic Period collapse of the Central Maya Lowlands: Insights about human–environment relationships for sustainability," Proceedings of the National Academy of Sciences, v. 109, p. 13908–13914.