Initial Publication Date: April 17, 2014

Mössbauer spectroscopy

by Sylvia-Monique Thomas, University of Nevada Las Vegas

Outline

Introduction
Theory
Instrumentation
Applications
Guest Lecturer
Literature
Related Links
Acknowledgements

Introduction

Rudolf Ludwig Mössbauer (31.1.1929 - 14.9.2011)

Show additional information

What is Mössbauer spectroscopy?

Mössbauer spectroscopy, named after the german physicist Rudolf Mössbauer, is used to study the local atomic environment around nuclei in a solid and thus provides information at the atomic level. In mineralogy Mössbauer spectroscopy is used to determine redox ratios, spin and valence state, and the site occupation (coordination polyhedra) of atoms in the crystal structure.

A calendar of the history of Mössbauer spectroscopy was put together by Prof. em. Leopold May of the Catholic University of America.

Advantages

· high energy resolution

· nuclide specific

· high nuclear cross section

· short range probe, allows studies of amorphous or poorly crystalline material

· in-situ studies at high P and/or T are possible

Theory

The Mössbauer effect

The Mössbauer effect describes the recoilless emission and resonant absorption of gamma radiation by atomic nuclei in solids [16].

If an atomic nucleus emits energy, in this case a γ quantum in a gas or a fluid the γ quantum looses the recoil energy E_R. This recoil energy is then transmitted back to the emitting nucleus for energy preservation. To enable absorption of the γ quantum by other atomic nuclei in a gas or liquid the energy of the γ quantum has to be increased by E_R. This is why recoilless emission and absorption in a gas or liquid are not possible.

In a solid, however, the recoil energy may be annihilated (E_R⇨0) and recoil-free emission and absorption become possible. There is a certain portion f of the emitting nuclei, the so-called recoil-free fraction (Debye-Waller factor, Lamb-Mössbauer factor), which is high enough in solids so γ rays can be emitted without loss of energy of the γ quantum. F becomes larger with decreasing Eγ, the recoil-free energy of the γ quantum, and decreasing χ², the mean square vibrational amplitude of the emitting nucleus in the direction of the γ ray. Another important parameter is the line width of the gamma ray, which depends on the lifetime of the nuclear excited state. A small line width allows the detection of small changes of the γ radiation energy, i.e. the detection of nuclear hyperfine interactions.

Hyperfine parameters

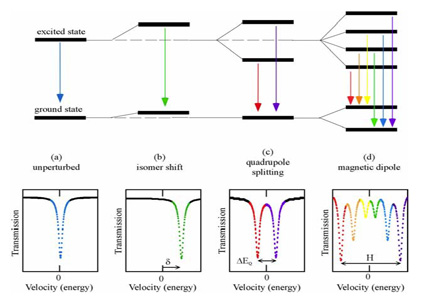
Hyperfine parameters

Show additional information

Hyperfine parameters describe interactions between nuclear moments and the surrounding electric or magnetic fields. Such hyperfine interactions observed with Mössbauer spectroscopy provide chemical, physical and crystallographic information. In Mössbauer spectroscopy three types of hyperfine parameters are considered, the isomer shift, magnetic hyperfine splitting and quadrupole splitting.

1) Isomer shift (chemical shift)

The total isomer shift (δ) or centre shift δ consists of δ₀ and δ_SOD. It depends on coordination, valence state and spin state of atoms and thus on s electron density and p and d electrons.

This shift of nuclear levels is caused by anelectrostatic interaction between the positively charged nucleus and the negative electronic charge . It is called isomer shift because it depends on the difference in the nuclear radii of the ground (g) and isomeric excited (e) states.

In Mössbauer spectroscopy the nuclear energy of the γ ray transitioning between two nuclear levels in the source is compared with that in the absorber, which differ because of different electronic and crystallographic environments. Energy differences as small as 10^-10 eV can be measured and δ₀ is calculated relative to a standard (e.g., for iron: isomer shift δ₀ of α-iron at room temperature). Using the difference in isomer shift δ₀ (i.e. distance between centroids of the doublets and the zero point of the velocity scale) for example Fe²⁺ and Fe³⁺ can be distinguished in a mineral. For Mössbauer nuclei, which have a smaller radius in the excited state than in the ground state, such as ⁵⁷Fe, the isomer shift δ₀ decreases with increasing electron density at the ⁵⁷Fe nucleus due to increasing valence or covalent bonding. For Mössbauer nuclei, which have a larger radius in the excited state than in the ground state, such as ¹¹⁹Sn, an increasing electron density leads to an increase of the isomer shift.

A second-order Doppler shift δ_SOD causes the temperature dependence of the isomer shift. δ_SOD depends on the force constant K and the mean square displacement χ² of the nucleus. As χ² increases with temperature, δ_SOD increases and the total isomer shift δ decreases.

2) Quadrupole splitting (QS or ΔE_Q)

The quadrupole splitting is a measure of the degree of crystallographic site distortion, the valence, spin state and coordination of the absorber atoms.

An electric quadrupole interaction, the splitting of nuclear energy levels, is caused by the interaction between the nuclear quadrupole moment Q (nuclear spin quantum number I > 1/2) and the non-cubic component of its surrounding electric field. In the case of ⁵⁷Fe the excited state of the ⁵⁷Fe nucleus is split, thus two nuclear transitions from the ground state to the excited states rather than just one occur. This results in two corresponding peaks in the Mössbauer spectrum. The energy difference between the two peaks describes the energy difference between the two excited states, i.e. the quadrupole splitting. The magnitude of the QS depends on the electric field gradient (EFG) q. The EFG is non-zero if the charge distribution around the nucleus (valence electrons and lattice ions) deviates from cubic symmetry.

3) Magnetic hyperfine splitting (ΔE_M)

A nucleus with a spin quantum number I > 1 has a non-zero magnetic dipole moment. Theinteraction of this nuclear magnetic dipole moment µ and a magnetic field H (internal or external) at the nucleus causes magnetic hyperfine splitting. In the case of ⁵⁷Fe the excited state (I =3/2) is split into 4 sublevels and the ground state (I=1/2) is split into 2 sublevels. This results in a peak sextet in the Mössbauer spectrum.

Instrumentation

Mössbauer spectrometer

Show additional information

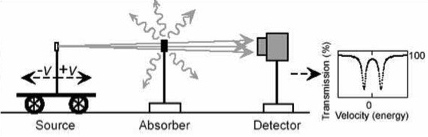
A Mössbauer setup consists of the source, the absorber (sample) and the detector. To vary the energy the Doppler effect is used by moving the source relative to the absorber.

Show Doppler effect

The Doppler effect (or Doppler shift) is named after and was proposed by the austrian physicist Christian Doppler in 1842 in Prague, Czech Republic. It describes the frequency change of a wave for an observer moving relative to the source of the wave.

The distance between two waves is called wavelength and the amount of time between waves passing is called frequency, which are interrelated by the wave traveling speed. High frequency indicates short wavelength and low frequency indicates long wavelength.

During the approach of a wave at the observer the received frequency is higher than the emitted frequency, it is identical when the wave passes by, and it is lower during the decay of the wave.

When the source of the waves is moving toward the observer, each successive wave is emitted from a position closer to the observer than the previous wave; each wave takes less time to reach the observer. The time between arrivals of waves at the observer is reduced, causing a frequency increase.

While traveling, the distance between waves is reduced; the waves bundle. On the other hand, if the source of waves is moving away from the observer, each wave is emitted from a position farther from the observer; the arrival time between waves is increased, the frequency reduced. The distance between successive wave fronts is increased, the waves spread out.

For waves that propagate in a medium, such as sound waves, the velocity of the observer and of the source are relative to the medium in which the waves are transmitted. The magnitude of the Doppler shift depends on the motion of the source, the motion of the observer, and the motion of the medium.

A linear geometry, with the detector arranged behind the source and absorber, is used for transmission studies to study all nuclei in the sample. A backscatter geometry in contrast can be used to study surface nuclei of the sample. The latter technique is called Conversion Electron Mössbauer Spectroscopy (CEMS) [15].

The source is a radioactive parent of a Mössbauer isotope, e.g. ⁵⁷Co is the parent of ⁵⁷Fe. An ideal Mössbauer source has a relatively low energy of the gamma radiation Eγ, thus a high recoil free fraction f, a long mean lifetime t of the first excited nuclear level, and thus a small half width G.

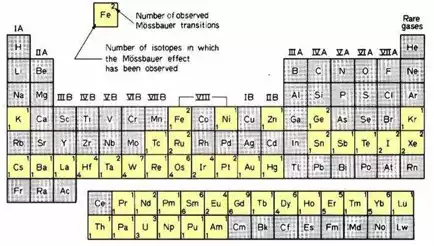
Mössbauer isotopes

Show additional information

A popular Mössbauer isotope is iron, because the half-life of its parent ⁵⁷Co is reasonable long (270 days), the natural line width is relatively small (0.097 mm/s), recoil-free fractions are generally high at room temperature and the absorption cross section is sufficiently high that reasonable spectra can be obtained even for absorbers with low iron concentrations. The source diameter for conventional ⁵⁷Co sources is in the order of 1 cm. It depends on the density of the parent nuclei and their number required for a sufficient count rate. Other suitable Mössbauer isotopes, such as ¹¹⁹Sn and ¹²¹Sb are highlighted in the periodic table.

The absorber, the sample, can be a powder, glass, single crystal, a melt or a liquid. The sample can be cooled, heated, measured under high-pressure or in an external magnetic field.

The detector can be a gas-proportional counter, a multi-channel analyzer combined with scintillation or semiconductor detectors, or a resonance counter.

Applications

· Mössbauer spectroscopy and synchrotron radiation

· Mössbauer spectroscopy and single-crystals in diamond anvil cells

Guest Lecturer

Literature

Review articles:

1) Amthauer et al. (2004) Mössbauer spectroscopy: Basic principles. In: Beran, A. & Libowitzky, E. (eds.) Spectroscopic Methods in Mineralogy. EMU Notes in Mineralogy, 6, 345-367.

2) Hawthorne, F.C. (1988) Mössbauer spectroscopy. In: Hawthorne, F.C. (ed.): Spectroscopic methods in mineralogy and geology. Reviews in Mineralogy, 18, Washington, D.C.: Mineralogical Society of America, 255-340.

3) McCammon, C. (2004) Mössbauer spectroscopy: Applications. In: Beran, A. & Libowitzky, E. (eds.) Spectroscopic Methods in Mineralogy. EMU Notes in Mineralogy, 6, 369-398.

Textbooks:

4) Bancroft, G.M. (1973) Mössbauer spectroscopy. An introduction for inorganic chemists and geochemists. New York (N.Y.): McGraw-Hill. ...

5) Dickson, D.P.E. and Berry, J.F (1986) Mössbauer spectroscopy. Cambridge University Press, 274 pp.

6) Gerdau, E. & de Waard, H. (1999) Nuclear resonant scattering of synchrotron radiation / Hyper. Inter. Spec. Issues, 123-124.

7) Gonser, U. (ed.) (1975) Mössbauer spectroscopy. Berlin: Springer-Verlag.

8) Greenwood, N.N. & Gibb, T.C. (1971) Mössbauer spectroscopy. London: Chapman & Hall, 659 pp.

9) Guetlich, Pl., Link, R. & Trautwein, A. (1978) Mössbauer spectroscopy and transition metal chemistry. Berlin: Springer Verlag.

10) Long, G.J. (ed.) (1984, 1987, 1989) Mössbauer spectroscopy applied to inorganic chemistry. Volumes 1-3, New York (N.Y.): Plenum Press.

11) Long, G.J. & Grandjean, F. (eds.) (1996) Mössbauer spectroscopy applied to magnetism and material science, vol. 2, Mod. Inorg. Chem. Ser./. New York (N.Y.): Plenum Press.

12) Marfunin, A.S. (1979) Spectroscopy, luminescence and radiation centers in minerals. Berlin: Springer-Verlag, 352 pp.

13) Shenoy, G.K. & Wagner, F.E. (1978) Mössbauer isomer shifts. Amsterdam: North Holland.

14) Wertheim, G.K. (1964) Mössbauer effect: Principles and applications. New York (N.Y.) Academic Press.

Applications:

15) Nomura, K. (1999) Conversion electron Mössbauer spectrometry. In Miglierini, M. & Petredis, D. (eds.): Mössbauer spectroscopy in material science. Dordrecht: Kluwer, 63-78.

Historic:

16) Mössbauer, R. L. (1958). "Kernresonanzfluoreszenz von Gammastrahlung in Ir¹⁹¹" (in German). Zeitschrift fur Physik A, 151 (2): 124–143.

17) Mössbauer, R. L. (1961) Recoilless nuclear resonance absorption of gamma radiation. Nobel lecture, December 11^th 1961.

18) The Rudolf Mössbauer Story

Acknowledgements

These materials are being developed with the support of COMPRES, the Consortium for Materials Properties Research in Earth Sciences, under NSF Cooperative Agreement EAR 10-43050 and is partially supported by UNLV's High Pressure Science and Engineering Center, a DOE NNSA Center of Excellence supported under DOE NNSA Cooperative Agreement No. DE FC52-06NA26274.