Ultrasonic Measurements

by Pamela Burnley, University of Nevada Las Vegas

Outline

Introduction 
Techniques
Guest Lecturer
Literature
Problem Set
Related Links

 

Introduction

The sound wave velocity as a function of depth in the earth is one of the few things that we can directly measure about the earth's interior. Models for the composition of the earth's interior are developed and validated by comparing measured sound speeds of candidate earth materials at pressure and temperature with what we observe for the earth.

The simplest way to measure sound speed in the lab is to introduce a sound wave into a long span of a material and then to observe how long it takes for the sound wave to get to the other end. There are a number of reasons why this approach is less than optimal, including the difficulty of finding a pure, crack free block of the material that is large enough to produce a measurable travel time. A variety of other strategies have been tried, but the one that is best suited for high pressure work is ultrasonic interferometry.

Ultrasonic Interferometry
 

The basic idea behind ultrasonic interferometry is to use interfering sound waves to measure the two way travel time through a specimen. When sound waves encounter the boundary between one material (A) and another (B) part of the energy of the sound wave will continue on through the A/B interface and part will be reflected back. The degree to which the energy in the wave is partitioned between the transmitted and reflected wave is a function of the impedance difference of the two materials; the impedance (Z) is a product of the sound speed and the density. The reflected waves will be in phase or out of phase by ½ wavelength (π) depending on whether the impedance of material A or B is higher. In the simplest ultrasonic interferometry design the sample is attached to a buffer rod. There is an echo created when the sound wave encounters the buffer rod/sample interface (BR), another echo (S1) when the sound wave reaches the interface between the sample and whatever is beyond (air, or for high pressure a confining medium). Generally the impedance of the buffer rod is chosen so that it is higher than that of the sample. In this case the returning wave is out of phase by π. This is also the case for the interface between the sample and whatever is on the other side of the sample. Therefore the wave returning off that interface (S1) is also out of phase by π. There are also internal echoes – so the first wave returning from the back surface (S1) will also produce a wave that reflects off the back surface and returns to the observer (S2). In this case the wave will not be out of phase because it does not change phase on the internal bounce. When the echoing soundwaves encounter the next pulse of soundwaves coming into the material they interact either constructively or destructively. In order for constructive interference to occur, the number of wavelengths between the surfaces of the sample must be an integer or half integer number. In practice the experimenter varies the time between the sound pulses while observing where the amplitude of the returning echoes is maximized and minimized. From this data, two way travel time can be calculated.

Ultrasonic work can be done on several scales depending on the sample size. In the multi-anvil samples are ~1 mm in length so an optimal wave length is in the Megahertz range. For diamond anvil cell samples which are on only ~100 microns in thickness Gigahertz frequencies are optimal 

Ultrasonic interferometry in the Multi Anvil

In the multi anvil the sound is introduced through the tungsten carbide (WC) anvil. A buffer rod connects the anvil to the sample which is sitting in the middle of the assembly inside the furnace. Thus there will be a reflection from the anvil/ buffer rod interface (AR) as well as the interfaces between buffer rod and the sample (BR) and the echoes from interface between the sample and the confining medium (NaCl). The multianvil allows the sound speed of both single and polycrystalline materials to be measured at high pressure and temperature. If the multianvil is at a synchrotron the length of the sample can be determined using radiography (as it is in the D-DIA), the temperature can be measured with a thermocouple, and the pressure can be determined via the EOS of the confining medium by measuring diffraction. The pressure limit of this technique is essentially the pressure limit of the multi-anvil. One of the big advantages of measuring the sound speed of polycrystalline samples in the multianvil is that the observed sound speed takes into account anelastic effects (e.g. viscous relaxation on grain boundaries and other defects) which cannot be easily anticipated from single crystal elastic constants. For more information on this technique see Baosheng Li's ultrasonics lab web page.

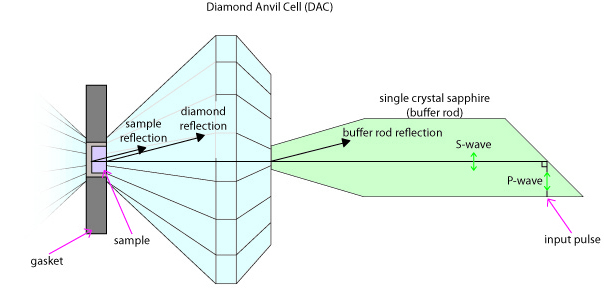
Ultrasonic interferometry in the Diamond Anvil Cell

Gigahertz ultrasonic interferometric experiments conducted in the DAC permit very tiny samples to be measured at pressures exceeding what can be achieved in the multianvil. A good place to learn about this technique is Steve Jacobson's web page

Guest Lecturer
 

"Ultrasonic Interferometry at High Pressures and Temperatures" Prof. Robert Liebermann

Part 1 (30 minutes) (MP4 Video 38.4MB Jul9 21)

Part 2 (25 minutes) (MP4 Video 33.7MB Jul9 21)

Part 3 (30 minutes) (MP4 Video 44.1MB Jul9 21)

Literature

Anderson, O.L., and Liebermann, R.C.. Sound Velocities in Rocks and Minerals: Experimental Methods, Extrapolations to Very High Pressures, and Results, in Physical Acoustics: Principles and Methods. Mason, W.P., ed. Academic Press, New York, 1968, p. 329-472.

Anderson, O.L., Schreiber, E., and Liebermann, R.C., (1968). Some Elastic Constant Data on Minerals Relevant to Geophysics, Reviews of Geophysics, 6(4), 491-524.

Jacobsen, S. D.; Spetzler, H. A.; Reichmann, H. J.; Smyth, J. R.; Mackwell, S. J.; Angel, R. J.; Bassett, W. A. (2002). Gigahertz ultrasonic interferometry at high P and T: new tools for obtaining a thermodynamic equation of state. Journal of Physics : Condensed Matter, 14, 11525-11530.

Li, B., and Liebermann, R.C., (2007). Indoor seismology by probing the Earth's interior by using sound velocity measurements at high pressures and temperatures, PNAS, 104(22), 9145-9150.

Li, B., J. Kung, and R.C. Liebermann, Modern techniques in measuring elasticity of Earth materials at high pressure and high temperature using ultrasonics in conjunction with synchrotron X-radiation, Phys. Earth Planet. Interiors, 143-144, 559-574, 2004.

Li, B., J. Kung, Y. Wang, and T. Uchida, Simultaneous equation of state, pressure calibration and sound velocity measurements to lower mantle pressures using multi-anvil apparatus, In: Frontiers in High Pressure Research: Geophysical Applications. Editors: J. Chen, Y. Wang, T. Duffy, G. Shen, L. Dobrzinetskaya, Elsevier, New York, pp.49-66, 2005.

Spetsler, H.A., Chen, G., Whitehead, S., and Getting, I.C. (1993). A new Ultrasonic Interferometer for the Determination of Equation of State Parameters of Sub-millimeter Single Crystals, PAGEOPH, 141 (2/3/4), 341-377.

Related Links

Baosheng Li at Stony Brook

Steven Jacobsen at Northwestern

Acknowledgements

These materials are being developed with the support of COMPRES, the Consortium for Materials Properties Research in Earth Sciences, under NSF Cooperative Agreement EAR 10-43050 and is partially supported by UNLV's High Pressure Science and Engineering Center, a DOE NNSA Center of Excellence supported under DOE NNSA Cooperative Agreement No. DE FC52-06NA26274.