What Constitutes a Complex System?
This summary was written by Carol Ormand, SERC.
- Feedback loops, where change in a variable results in either an amplification (positive feedback) or a dampening (negative feedback) of that change
- Many strongly interdependent variables, with multiple inputs contributing to observed outputs
- Chaotic behavior: extreme sensitivity to initial conditions, fractal geometry, and self-organized criticality
- Multiple (meta)stable states, where a small change in conditions may precipitate a major change in the system
- A non-Gaussian distribution of outputs, often where outcomes that are far away from the average are more likely than you might think
Systems Consist of Components and Their Relationships
Examples are as diverse as the global economy, the human nervous system, ecosystems, the climate system, and the Earth system. The Earth system consists of the atmosphere, hydrosphere, biosphere, and lithosphere (solid Earth, including the soil) and the interactions among those spheres.
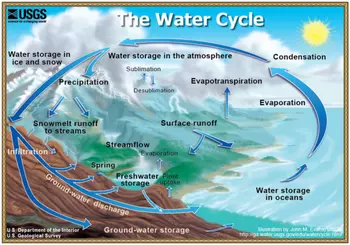Diagram of the hydrologic (water) cycle, courtesy of the U.S. Geological Survey. Click on the image to see a larger version. Cycles Within Systems
One way to examine a system is to study the movement of material within it. For example, the hydrologic cycle tracks the movement of H2O through the Earth system. Water may be temporarily stored in the atmosphere (in clouds), in the hydrosphere (in the oceans, rivers, lakes, or other surface waters, or in snow or glacial ice), in the biosphere (in plants, animals, or other living organisms), or in the lithosphere (in groundwater, soil, pore spaces in bedrock, or even within "hydrous" mineral grains in solid rock). Water moves from one sphere to another through a wide variety of processes. Any place water can be stored is a called a reservoir; the motion of water from one reservoir to another is called a flux. On the diagram to the right, the words and arrows represent fluxes. More generally, any cycle can be depicted as a collection of reservoirs with a set of related fluxes. The water cycle is a small, but significant, part of the Earth system. Learn more about what constitutes Systems Thinking from InTeGrate.
Feedback Loops Can Amplify or Dampen Change
Feedback mechanisms have been described as a threshold concept for understanding complex systems, a concept "difficult to learn but transformative once mastered" (Kastens et al., 2009). A feedback loop is a mechanism by which change in a variable results in either an amplification (positive feedback) or a dampening (negative feedback) of that change.
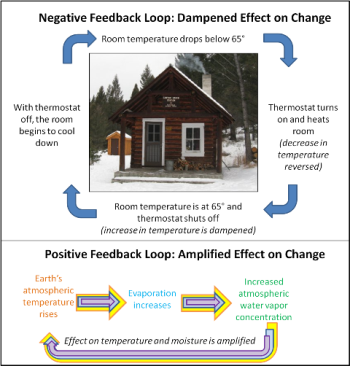Diagram of negative and positive feedback loops. Image by Monica Bruckner.We are familiar with feedback in our everyday lives in many contexts. For example, a thermostat uses feedback to regulate air temperature within a building. During the winter, a rise in temperature to the desired level signals the thermostat to turn off the furnace (dampening the increase in temperature = negative feedback). This causes the temperature within the building to stabilize, and then to begin to cool as heat is lost to the exterior. This signals the thermostat to turn the furnace on again (also a negative feedback, because it reverses the decrease in temperature). Negative feedbacks act to maintain a system's current, stable state.
Positive feedback mechanisms, in contrast, act to amplify change. For example, when the Earth's atmospheric temperature rises, evaporation increases, which causes an increase in atmospheric water vapor concentration, which causes an additional rise in atmospheric temperature through the greenhouse effect, which causes more evaporation, and so on. If there were no other factors contributing to atmospheric temperature, this rise in temperature would spiral out of control. Fortunately for life on Earth, there are many factors that affect the temperature of our atmosphere.
In addition to the challenges presented by the concept of feedback loops, the terminology itself can confuse students, who may think that "positive" feedback is good and "negative" feedback is bad. This misunderstanding is exacerbated by common (mis)usage of those terms (Kastens, 2010).
Strongly Interdependent Variables: Changes Can Have Unintended Consequences
In a complex system, there are many variables, and they are strongly interdependent. This makes it difficult to know exactly which inputs contribute to an observed output, and the extent of each factor's contributions. For example, an increase in the average global temperature can be caused by changes in the solar radiation budget, changes in the composition of the atmosphere (such as a change in the concentration of water vapor), changes in the Earth's albedo (the amount of solar radiation reflected by snow and ice cover), or a combination of all of those factors. Moreover, those factors are not independent of one another: changes in atmospheric composition can lead to changes in precipitation rates, which can lead to changes in the percentage of land covered by snow and ice, thus changing the Earth's albedo.
Because the variables in a complex system are so strongly dependent on each other, changes to system inputs can have unintended, unanticipated consequences. This is one reason why accurate prediction of the behavior of complex systems is so difficult. (Some climate change deniers use this to argue that human impacts on climate are still debatable. Climate scientists, however, overwhelmingly agree that our global climate is changing as the result of human activities (IPCC, 2007 (more info) ).) Examples of such unanticipated consequences brought about through human interaction with complex systems range from the proliferation of antibiotic-resistant bacteria to fluctuations in the global economy.
Complex Systems Exhibit Chaotic Behavior
Chaotic behavior is characterized by extreme sensitivity to initial conditions, fractal geometry, and self-organized criticality (Turcotte, 2006).
Sensitivity to initial conditions
The concept of sensitive dependence on initial conditions has been popularized in the so-called "butterfly effect": the idea that a butterfly flapping its wings in Brazil could change the weather in Texas. Minute differences in the initial conditions for such a system result in extremely different outcomes. Edward Lorenz discovered this property while studying thermal convection (Lorenz, 1963), and from it correctly inferred the difficulty of long-term weather prediction. The butterfly effect refers to the idea that the flap of a butterfly's wings would be enough to change the initial conditions of the Earth's atmosphere, thus having a profound effect on global weather patterns. While this may seem far-fetched, it begins to make sense when you consider the strong level of interdependence of the system, its nonlinearity, and the possibility for signal amplification via feedback.
Fractal geometry
Benoit Mandelbrot coined the term "fractal" to describe a special set of self-similar curves. Self-similarity implies that an object looks the same at any scale. Many natural objects approximate fractal geometry, such as clouds, snowflakes, river drainage systems, and coastlines. In fact, geographic coastlines are "so involved in their detail that their lengths are often infinite or more accurately, undefinable" (Mandelbrot, 1967). Mathematically, self-similarity requires a power-law distribution of representative objects. In other words, as the size of an object decreases, there is a corresponding power-law increase in the number of objects of that size. For example, the ratio of second-order streams to first-order streams in a drainage basin is very nearly equal to the ratio of third-order streams to second-order streams, or to the ratio of fourth-order streams to third-order streams, and so on (Turcotte, 2006).
Self-organized criticality (SOC)
Self-organized criticality is the concept that a dynamic system will move toward a critical, or emergent, state, by natural processes. It is perhaps most easily understood via an example. This concept was introduced by Bak, Tang and Wiesenfeld in 1988 to explain the behavior of a cellular automaton (CA) model. In their model, sand is dropped randomly into a square array of boxes (cells). Sand grains accumulate in each box until it holds four grains. At that point, the four grains are redistributed: one to each of the four nearest neighboring boxes. If the addition of those grains to the neighboring boxes triggers another redistribution, the chain reaction is referred to as an avalanche. Simulations of this model show that the size of the avalanches (number of boxes involved in chain reaction events) follows a power-law distribution. Moreover, many natural events (including avalanches, landslides, forest fires, and earthquakes) have been found to exhibit power-law frequency-area behavior (Bak et al., 1988, cited in Turcotte, 2006).
Mound of gravel at the angle of repose. Click on the image to see a larger version. Image from Wikimedia Commons. 
The critical, or emergent, state of a natural sand pile is a circular cone where the sand surface has reached the angle of repose. In that state, the addition of sand will lead to an avalanche of some size, thus maintaining the angle of repose (and the conical shape of the pile). The system, or sand pile, achieves this state -- a metastable, or "critical" state -- through a series of avalanches, without any interference from external forces or processes. This is what is meant by "self-organized" criticality (Herbert, 2006).
Multiple (Meta)stable States: Small Changes Can Cause Major Consequences
Metastability describes a system that is in a delicate state of equilibrium -- a state where a small change in conditions may precipitate a major change in the system. The chaotic nature of complex systems -- and particularly their sensitivity to initial conditions -- means that they are often either not in equilibrium or are metastable. The alternation of Ice Ages and Interglacial periods over the past two million years of Earth's history suggests that these two climactic conditions are metastable states for our planet.
A Non-Gaussian Distribution of Outputs: "Unlikely" Events Are Less Unlikely
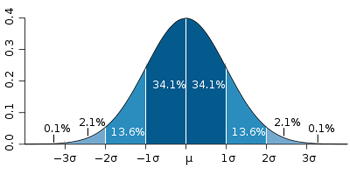
A "normal," or Gaussian distribution is a bell-shaped distribution clustered around an average, such as that shown in the graph on the right. A non-Gaussian distribution is, literally, any distribution that is not Gaussian. However, it often refers to a distribution with "heavy tails," where those outcomes that are far away from the average are more likely than they would be in a Gaussian distribution. Complex systems exhibit non-Gaussian outputs.
What this means in practice is that "improbable events are orders of magnitude more likely than events that follow the Gaussian distribution. Estimates and predictions of system future behavior, particularly Gaussian estimates, formed by observations collected over short time periods provide an incorrect picture of large-scale fluctuations" (Herbert, 2006). This is true for all kinds of complex systems, from financial systems to Earth systems.
References
Bak, P., Tang, C. & Wiesenfeld, K. 1988. Self-organized Criticality, Phys. Rev. A, v. 38, p. 364-374.
Herbert, 2006. Student Understanding of Complex Earth Systems. In C. Manduca and D. Mogk (Eds.), Earth and Mind: How Geologists Think and Learn about the Earth : Geological Society of America Special Paper 413, p.95-104.
Intergovernmental Panel on Climate Change, 2007. Climate Change 2007: Synthesis Report (more info) . Online at http://www.ipcc.ch/publications_and_data/publications_ipcc_fourth_assessment_report_synthesis_report.htm; accessed 4 December, 2009.
Kastens et al., 2009. How Geoscientists Think and Learn. Eos, Transactions, v. 90, n. 31, p. 265-266.
Kastens, 2010. Going Negative on "Negative Feedback." Earth and Mind blog: http://serc.carleton.edu/earthandmind/posts/negativefeedbac.html. Accessed February 17, 2010.
Lorenz, 1963. Deterministic Nonperiodic Flow. Journal of Atmospheric Sciences, v. 20, p. 130-141.
Mandelbrot, 1967. How Long is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science, v. 156, p. 636-638.
Roe, 2009. Feedbacks, Timescales, and Seeing Red. Annual Review of Earth and Planetary Sciences, v. 37, p. 93-115.
Turcotte, 2006. Modeling Geocomplexity: "A New Kind of Science." In C. Manduca and D. Mogk (Eds.), Earth and Mind: How Geologists Think and Learn about the Earth : Geological Society of America Special Paper 413, p.39-50.
USGS, The Water Cycle. Online at https://water.usgs.gov/edu/watercycle.html; accessed 16 September, 2009.
Winslow, 1997. Introduction to Self-Organized Criticality & Earthquakes. Online at ftp://ftp.ingv.it/pro/terrasol/materiale_consultazione/SOCEQ.pdf; accessed 07 July, 2016.