Why Do Geologists Use Graphs?

Initial Publication Date: October 10, 2007

Quantitative concepts: Basic graphing skills, exponential growth and decay

Why Do Geologists Use Graphs?

by Jennifer M. Wenner, Geology Department, University of Wisconsin-Oshkosh
Jump down to: Functions | Use of Graphs | Good Ideas | Examples and Exercises

Essential Concepts

Many students in introductory geoscience courses have a hard time with plotting and graphing. Although most faculty assume (and rightly so) that these students have had exposure to graphing and plotting data, it often becomes apparent within the first few labs or lectures that many of them struggle with the concepts. To help them with the idea of plotting data on graphs, there are five important concepts to incorporate into the review/help:
  1. remind them of the skills they may have learned in high school (or earlier),
  2. point out that whereas mathematicians often use functions to derive data, geologists often use data to derive functions (equations),
  3. give them reasons that we use graphs to help us understand data,
  4. teach about graphs using the good ideas from Mathematics Education to help them understand connections and tools.

Reminding students what graphs represent

In many geologic applications basic graphing involves the Cartesian coordinate system; thus, to refamiliarize them with these skills, they need to be reminded that:
  • there are two axes - horizontal (often called the x-axis) and vertical (often called the y-axis),
  • a point on the graph is denoted by an ordered pair (or coordinates (e.g., (3,8)) where:
    • the first number refers to horizontal position on the x-axis,
    • the second number refers to vertical position on the y-axis,
  • the two axes intersect at point called the origin which has the coordinates (0,0),
  • the reason that we plot data is so that we can more easily observe trends or behavior of the data
    • (modified from Anderson and Swanson, 2005)

Data from functions or functions from data?

There are two ways that graphs can be used: (1) to display a known relationship (i.e., generating a graph from a function) and (2) to display an unknown relationship between variables (i.e., fitting a function to empirical data). In math classes (and even using their calculators), many students will know how to plot (and even to generate data from) a function. However, many useful graphs in the geosciences use empirical or experimental data to generate an equation (or function) that describes the relationship of physical variables. How this is done may not be immediately apparent to students and faculty may need to explicitly point this out.
Plots of basic x-y data involve functions. An example of a basic function that is often plotted is that of a line:
y = mx + b
Tables of data that solve this equation can be generated by arbitrarily assigning a value to x or y or, alternatively, data can be used to derive an equation that describes a dataset.
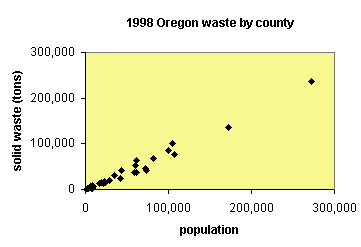plot of data from QELP comparing population to tons of solid waste
For example, in town or city planning, we might want to know how much area is (and will be) needed for waste disposal. To do this, we need to know the relationship of population to amount of solid waste generated. QELP (more info) has a set of data for Oregon showing how waste increases with increasing population. Generally, the increase is linear. We can fit a line to the data and describe it with the equation:
y = 0.87x
where y = solid waste in tons and x = population (and the y-intercept (b) = 0 because zero people generate zero waste). This suggests that each additional person in a town will increase the waste generated by approximately 0.87 tons in one year! To plan for waste disposal and growth, these factors need to be taken into consideration.

Why use graphs?

As discussed above, often the relationship between physical variables is not well know (or so complicated that it varies by situation). Geologists are interested in predicting and understanding the physical way that the Earth works. For us, plotting data and sketching the relationship among variables helps us to understand and predict the behavior of the Earth in different situations. However, the Earth is a very complicated (and varied) place. Often times we need to simplify it to make it easier to understand. An example of this concept is presented in the forecasting sections of SERC's floods and flooding page.
When talking about models of the physical world (because, after all, graphs are really just simplified models of data), it is important to understand the assumptions and simplifications that have gone into the model. For example, if we want to talk about the likelihood of a river flooding, what kinds of variables do we need to take into account? Thinking about rivers that you know, what affects their ability to flood the ground around them?
Flood Frequency Analysis
  • topography
  • drainage area
  • rainfall
  • permeability of the drainage area
  • vegetation
  • and many other things
Yet when we talk about flooding, we generally talk about how much water is flowing through the channel (at a given point) and how often that happens. We have simplified a very complex system into two variables. Why can we do this? If we had to take ALL those things into account, the system (and the graph) would be so complicated, we might not be able to understand it. However, when we simplify it, it approximates the system well enough so that we can understand it.

Geologists use graphs in a variety of ways. As mentioned above, graphs can be a visual way of predicting or forecasting geologic events. But they are also used to understand the behavior of systems, to visualize large sets of data and to help geologists understand many important systems that might not be as easy to understand just by looking at a bunch of numbers. Graphs are a way of making scores of data points manageable and, often, more understandable.

Good ideas for teaching graphing

There are a number of good ways to convey quantitative concepts to students. Two other pages deal with the "good ideas" when it comes to helping students to quantitatively understand graphs and plots and the ways that geologists use them.

Examples and Exercises