Geologic context: Waves (ocean and seismic), dunes and wind, subduction zones, strike and dip, compass directions, and many more...

Trigonometry and Angles

Jump down to: Teaching strategies | Materials & Exercises | Student Resources

What's so hard about angles and trigonometry?

An understanding of angles and the ability to manipulate trigonometric expressions is essential for the introductory geoscience student. Geoscientists use both of these concepts in numerous applications, from coastal geology to mineralogy to geologic mapping. Helping students to develop the tools they need to understand these important concepts can be challenging. Most college students have learned about trigonometry at some point in their high school career (remember "soh, cah, toa? sin = opposite/hypotenuse..."); however, moving beyond the abstract mathematics to application is often difficult for the student.

Teaching Strategies: Ideas from Math Education

Put quantitative concepts in context

Trigonometry and angles are used in a wide variety of geoscience topics, including:

Show caption

Hide

Waves refracting as they approach shore. Courtesy Steve Dutch's Coastal Geology slides page. Details

Geologic structures and mapping
Compass direction, strike and dip
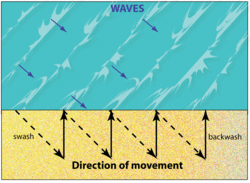
Ocean and seismic waves
Dunes, wind direction and currents
Subduction zones
Slope stability
Planetary applications (parallax)

Use multiple representations

Because everyone has different ways of learning, mathematicians have defined a number of ways that quantitative concepts can be represented to individual students. Below are some ways that angles and their relationship to trigonometry are used in geoscience concepts.

graphical/visual representation

Show credits

Hide

Example of coordinate systems (both degrees and radians) from the Geomaths (more info) page

Commonly, students will have encountered angles in degrees: "an angle of 90°", for example. In mathematics, the coordinate system used to talk about angles is a "right-handed" coordinate system - 0° and 180 ° are parallel to horizontal and 90° and 270° are parallel to vertical. Angles increase going counterclockwise from horizontal (in other words, 3 o'clock is 0°, noon is 90°, etc.).

Show caption

Hide

Compass showing the left-handed coordinate system used in geosciences for direction. Details

As if angles and trigonometry weren't confusing enough - for geologists, the coordinate system is turned on its side and flipped over (it's left-handed). Compass directions are arranged like a clock - 0° (north) is at 12 o'clock, 90° (east) is at 3 o'clock, 180° (south) is at 6 o'clock and 270° (west) is at 9 o'clock.

This distinction may seem superfluous since in trigonometry an angle of 90° give the same results no matter the direction. However, the distinction between right- and left-hand coordination systems becomes extremely important for map reading (particularly when we get to reading structural information from a geologic map). To avoid confusion, a simple discussion of the distinctions between map angles and math angles is worthwhile before beginning an exercise in which students have to use structural information.

There are two ways that students may struggle with these distinct coordinate systems:

Students who are uncertain of their math skills will need help with the idea of a coordinate system. Giving students a compass (a sketch on paper will do) with angles and directions labeled on it may help them to visualize the organization of the coordinate system used in geology.

Clocks are also left-handed, like a compass. Details

On the other end of the spectrum, students who have taken a number of math courses (particularly trigonometry) will need help adjusting to a new system. Taking time to explain the organization in relation to a clock (something that all students can relate to) may help them to make the transition.

Acknowledging and recognizing differences (and similarities) between the two types of coordinate systems can make these ideas less intimidating to students.

numerical representation/angle units

As if two coordinate systems weren't confusing enough for the geoscience student, geologists and mathematicians often use two different systems to express angular measurements: degrees and radians.

As discussed above, geologists (and sometimes mathematicians) generally use degrees for measurement of angles. A circle has 360° total; a right angle is 90°. The orientation of 0° and other angles varies for geologic and mathematical applications (see graphical representation). Geologists use circle geometry to talk about compass directions where 0° is at 12 o'clock and angles increase in the clockwise direction.

Show caption

Hide

Diagram illustrating the way that sediment moves along the beach with longshore transport. Diagram drafted by J. Wenner. Details

Geoscientists also talk about angles in degrees when we talk about orientation of one line (or vector) to another. Examples of this include: relative plate motions, wave propagation and slope stability. For these applications we use triangle geometry to describe these directions.
Mathematicians often use radians to measure angles. The radian is the standar unit of angular measurement. Radians are units of angular measure defined such that the circumference of a unit circle (with a radius of one) is equal to 2π (in other words, one radian is equal to 180/π or approximately 57.3 degrees). An entire sweep around a unit circle is 2π radians; thus, a right angle is π/2 radians. Radians are rarely used in geoscience - the most common problem that students encounter is that they have not changed their calculators to degrees.

symbolic representation

Most students will be familiar with the right triangle definitions of these functions (sine, cosine and tangent are abbreviated sin, cos, and tan, respectively):

Right triangle geometry. Details

sin θ = opposite/hypotenuse ,

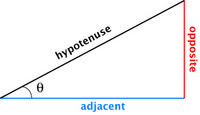
cos θ = adjacent/hypotenuse

and

tan θ = opposite/adjacent

where θ is the angle of interest; opposite, adjacent and hypotenuse represent sides of the triangle. See figure at right for illustration of right triangle geometry.

This is probably the most common way that trigonometry is used in introductory geology; for example, the use of angles in seismic and ocean wave refraction or slope stability. In geoscience classes, students are often asked to rearrange and solve these equations using vectors.

physical representation

Model to illustrate angle of repose. Click to enlarge. Details

A great way to help students to understand the concept of angles is to give them a physical representation of the angle itself. A simple model using a board with a hinge (or even just something to prop it up at an angle) can be constructed to illustrate topics such as angle of repose or strike and dip. In this way, students can physically measure angles and can visualize what the mathematics mean in physical reality.

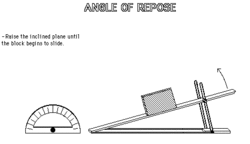
To expand on the physical model and include some mathematical calculations, trigonometry could be added to an exercise on angle of repose using the mass of an object placed on the board. Trigonometry can be used to calculate the normal force and the shear force exerted on the object for a given angle.

Use technology appropriately

Students have any number of technological tools that they can use to better understand quantitative concepts -- from the calculators in their backpacks to the computers in their dorm rooms. Students can make use of these tools to understand both right triangle geometry and trigonometric functions.

Graphing calculators

Graphing calculators are an easy way for all students to calculate trigoniometric functions and to better understand angles and their relationship to vectors. All graphing calculators are slightly different and students may need help with their particular model. There are some helpful hints for some calculators at Prentice-Hall's Calculator help website (more info) .

Because angles can be measured in both degrees and radians, calculators can be set to calculate trigonometric functions for either of these units. Radians are most commonly used in the mathematics courses. Since students generally buy calculators for use in mathematics class, their calculators may be set to calculate in Radians. Make sure that students check to make sure that their calculators are set to the degree mode. I try to remember to remind students to make the change before they start working on an exercise using angles and trigonometric functions. Although models will differ, students usually have a good idea of HOW to set their calculators.

University of Central Florida has some activities for a Casio calculator including some on dynamic graphing of the sine and cosine functions.

Computers

Spreadsheet programs provide good ways to keep track of a large quantity of angular measurements and these can easily be converted from degrees to radians (or vice versa). Several of the activities in the activites collection make use of spreadsheets to reinforce trigonometric concepts. Calculations of trigonometric functions are also relatively easy with simple commands. However, one drawback to many spreadsheet programs is that they have neither formatting for angular measurements (degrees, minutes, seconds) nor the ability to plot data on polar diagrams. Students are likely to encounter spreadsheet programs in many of their classes and the graphing capablilties are excellent tools for visualizing the shape of an equation.

Work in groups to do multiple day, in-depth problems

Mathematicians also indicate that students learn quantitative concepts better when they work in groups and revisit a concept on more than one day. Therefore, when discussing quantitative concepts in entry-level geoscience courses, have students discuss or practice the concepts together. Also, make sure that you either include problems that may be extended over more than one class period or revisit the concept on numerous occasions.

Geoscience concepts reinforce trigonometric functions numerous times within one introductory course. Topics include angle of repose, wave refraction, the behavior of seismic waves in the Earth and measuring strike and dip. A detailed discussion is necessary when the concept is first introduced and some mathematical review will likely be necessary. However, when another topic related to trigonometry comes up, remind students of topics where the same mathematical skill is useful. Students are more likely to retain mathematical material when they see connections among topics.

Teaching Materials and Exercises

Modeling the interior of the Earth using Seismic Waves
An assessment of Hillslope Stability
Rock Density - some applications
Scaling Galileo's solar system

Student resources

Geomaths modules (more info) are designed to help students with mathematics relevant to geoscience. The Notebook on Trigonometry includes exercises about finding the true width of strata, cliff erosion, and seismic waves.
MathWorld has dozens of pages relating to trigonometry (more info) , including some examples of problems and applications.
S.O.S. Mathematics has a trigonometry index (more info) , featuring a table of trigonometric identities, lessons on functions and formulae, and a section of exercises and solutions.
Math Help's trigonometry index (more info) provides a good refresher on basic trig identities, functions and angles. Also includes diagrams for unit circle and triangle trigonometry.
Maths online (from Austria) has some java resources to help students understand trigonometric functions.
The AP Calculus class at Batesville High School in Indiana has a Trigonometry Review with questions about right triangle trigonometry.

« Previous Page Next Page »