Diffusion and Partitioning
by Sylvia-Monique Thomas, University of Nevada Las Vegas
Outline
Introduction
Theoretical Aspects
Analytical Techniques
Types of Diffusion
Guest Lecturers
Literature
Additional Literature
Related Links
Introduction
What is diffusion?
Diffusion is the transport process by which atoms, ions or molecules dissolved in a medium, such as minerals, glasses, melts, gases or fluids, migrate. Diffusion describes mass transport, which happens in the absence of bulk flow and is due to thermally activated random motion of particles. At any temperature that is unequal to absolute zero atoms are in motion, independent of their aggregation state. In diffusion reactions particles migrate from places of higher concentration to those of lower concentration.
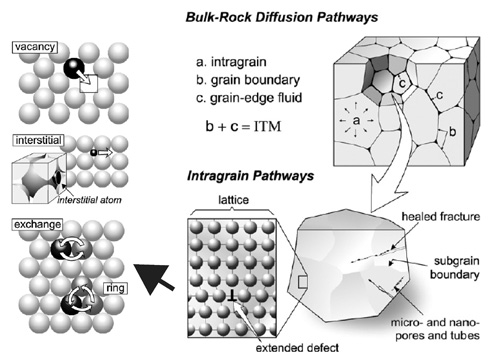Schematic of diffusion mechanisms (left) and pathways in rocks and mineral grains (right). Click for larger image.
Show additional information
HideWhat is partitioning?
Many elements occur in rocks in low concentrations and are not able to build their own minerals. However, they can enter mineral structures, with certain elements being incorporated preferentially. This process is called element partitioning. Element partitioning can be described by the partition coefficient, D (sometimes K), which is the concentration ratio of an element between two phases. Note that the letter "D" is used both for diffusivity and partition coefficient but describes two totally different processes. The partition coefficient depends on factors such as composition, temperature and pressure, but is independent of the element concentration.
The partition coefficient can be calculated using the following equation: D = CA / CB, where CA is the concentration of an element in phase A and CB is the concentration of an element in phase B. A value of D > 1 indicates that the element is compatible, it is preferentially accepted by the mineral. A value of D
In 1855 the German physician and physiologist Adolf Eugen Fick (1829-1901) introduced Fick's law of diffusion, describing diffusion of a gas across a fluid membrane, and thus the relationship between diffusion flux of a component and its concentration gradient. Albert Einstein (1879-1955) continued working on the relationship between random atomic movement and the process of diffusion. Diffusion has been of interest in a diversity of fields since then, such as physics, metallurgy and chemistry.
Applications
In geology the study of diffusion is used to understand magmatic and metamorphic processes, mass transport, fluid/rock interactions, thermal and physico-chemical history of rocks and crystal growth, mineral zonation, atom ordering, exsolution features and isotopic characteristics. Diffusion is a microscopic process, which can lead to macroscopic effects. A common example is the initial phase of explosive volcanic eruptions, in which diffusion controls bubble growth by allowing gas molecules to migrate into bubbles.
Theoretical Aspects
Fick's Laws
In each diffusion reaction the flux of matter equals the conductivity multiplied by a driving force, with the conductivity being the mobility of the diffusing species (diffusivity) and the driving force being the presence of a concentration gradient as a function of distance in a direction (where a constant concentration gradient depicts a linear variation of concentration in one direction).
There are two types of diffusion reactions, steady-state and nonsteady-state. The former takes place at a constant rate, which means the flux of particles crossing a certain interface is constant with time; in the latter reaction the diffusion rate is a function of time.
1) Fick's first law (steady-state diffusion equation) describes the relationship between diffusive flux and concentration gradient. Random motions of particles cause an initially heterogeneous phase to reach a state of homogeneity. The diffusive mass flux of a species is proportional to the present concentration gradient:
,
where J is the diffusive mass flux of a species (a vector), D is the diffusion coefficient (diffusivity), C is the concentration of the diffusing species in mass per unit volume, x is the distance, ∂C/∂x is the concentration gradient (a vector), and the negative sign indicates that the direction of the diffusive flux is opposite to the direction of the concentration gradient. Diffusive flux goes from regions of high concentration to low concentration with the gradient going the opposite direction, from low to high concentration. Fick's first law is a one-dimensional equation, i.e., concentration gradients in directions other than x are assumed to be zero.
In reality the steady state rarely holds. In order to determine how a concentration profile will evolve with time another equation is needed, the one-dimensional diffusion equation, mass conservation equation or Fick's second law (nonsteady-state equation). The rate of compositional change is proportional to the 'rate of change' of the concentration gradient and not the concentration gradient itself:
,
where D is independent of C and x. It describes how the concentration is related to space and time with a given initial concentration distribution. The diffusion distance x is proportional to the square root of duration
.
2) Effect of temperature
A temperature increase leads to a greater particle mobility. Diffusivity increases rapidly with temperature; it follows the Arrhenius relation:
where T is the temperature in K, D0 is the diffusivity, E is the activation energy (positive) and R is the gas constant. D0 and E are temperature-independent constants.
3) Effect of pressure
The pressure dependence can be either positive or negative. The following equation is use to describe both the temperature and pressure dependence of D:
where ∆ V is the activation volume. The activation volume can be positive (D decreases with increasing pressure) or negative (D increases with increasing pressure), it depends on the diffusion mechanism. The activation energy E depends on pressure.
4) Diffusion coefficients
The value of diffusivity describes the 'rate' of diffusion. Diffusivity depends on factors, such as temperature, pressure, composition, physical state, structure of the phase, and oxygen fugacity.
Typical diffusion values (from high to low):
a) Gas: D ~ 10-5 m2/s in air at 300 K
b) Aqueous solution: D ~ 10-9 m2/s in water at 300 K
c) Silicate melt: D ~ 10-11 m2/s at 1600 K for divalent cations
d) Mineral: D ~ 10-17 m2/s at 1600 K for divalent cations
The rate of diffusion on surfaces is higher than along grain boundaries, which in turn is much higher than that of volume diffusion. Diffusivities of alkali ions are in general higher than those of oxygen and alkali-metallic ions, such as silicon, which is due to different bonding strengths.
Analytical Techniques
The goal of all diffusion experiment is to control the environment around the sample, such as temperature, pressure, fugacities (oxygen, hydrogen, water) in order to measure reaction kinetics. The sample can be placed in a furnace or in a sealed sample container with buffers and water. For the study of diffusion profiles of deep Earth minerals, the sample can be loaded for example in a piston-cylinder press, a diamond anvil cell or a multi-anvil apparatus, or in an internally-heated pressure vessel.
There are bulk powder-fluid exchange experiments, where only an exchange average as a function of time is the result of the study, and experiments on single-crystals, which can be either mass-loss experiments (successive heating) or directly measured diffusion profiles (single continuous heating event).
Samples can be analyzed using following techniques:
- Electron microprobe analysis (EMPA)
- Secondary ion mass spectrometry (SIMS)
- Laser ablation inductively coupled mass spectrometry (LA-ICP-MS)
- Rutherford backscattering spectroscopy (RBS)
- Nuclear reaction analysis (NRA)
- Elastic recoil detection (ERD)
- Infrared and Raman spectroscopy
- Synchrotron X-ray fluorescence microanalysis (µ-SRXRF)
Types of Diffusion
When the word 'diffusion' is mentioned without further explanation, diffusion describes the volume diffusion in a system due to thermally induced random motion of particles. Note that in literature diffusion definitions differ a lot. For a discussion of other definitions than those listed below, see Zhang (2010). Generally, diffusion is classified based on either the diffusion species or the diffusion medium.
Diffusion medium-based classification:
1) Volume diffusion: Diffusion within a system, where the diffusion medium can be either isotropic or anisotropic. In the former diffusion properties do not depend on direction. Examples are melts, glasses and isometric minerals.
Example: diffusion of Mg and Fe2+ in a garnet crystal
2) Grain-boundary diffusion: Diffusion along interfaces, such as interfaces between the same minerals, different minerals or mineral-fluid interfaces. This kind of diffusion is generally related to a high defect concentration, diffusivities are usually higher than those related to volume diffusion.
Example: Si diffusion at forsterite-forsterite grain-boundaries
Diffusion species-based classification:
3) Self diffusion: Random displacement of atoms in the absence of chemical gradients.
4) Tracer diffusion: A tracer, for example a radioactive isotope, is introduced into a uniform system with an undefined low concentrations. Condition is, that there are no major concentration gradients. If a component has a very high solubility in the host material it may lead to significant chemical potential gradients. The tracer can also be a trace element. The diffusivity is assumed to be constant, which means it does not depend on the concentration of the component itself at low concentrations. This is true for many components with the exception of H2O, its diffusivity depends on its own concentration even at low concentrations (tens of ppm).
5) Chemical diffusion: A chemical potential (µ) gradient is present in major and minor components.
Trace element diffusion: Trace element diffusion in the presence of concentration gradients of major oxides such as SiO2 or MgO. Trace element concentration is less than thousands of ppm.
Interdiffusion (binary diffusion, mutual diffusion):Diffusion in a binary system, such as MgO-SiO2.
Multispecies diffusion: Diffusing component is present in two or more species, such as for example H2O present as H2O molecule and OH groups.
Multicomponent diffusion: Three or more components are diffusing in a system (melt, mineral).
Guest Lecturers
"Diffusion and Partitioning" Prof. Wendy Panero and Prof. Rick Hervig
Part 1 (35 minutes) (MP4 Video 38.5MB Aug26 24)
Part 2 (45 minutes) (MP4 Video 56MB Aug26 24)
Part 3 (20 minutes) (MP4 Video 24.9MB Aug26 24)
Literature
1] Watson, E.B. & Baxter, E.F. (2007) Diffusion in solid-Earth systems. Earth and Planetary Science Letters, 253, 307-327.
2] Béjina, F., Jaoul, O. & Liebermann, R.C. (2003) Diffusion in minerals at high pressure: a review. Physics of the Earth and Planetary Interiors, 139, 3-20.
3] Ganguly, J. (2002) Diffusion kinetics in minerals: Principles and applications to tectono-metamorphic processes. EMU Notes in Mineralogy, 4, 10, 271-309.
4] Zhang, Y. (2010) Diffusion in minerals and melts: Theoretical Background. Reviews in Mineralogy and Geochemistry, 72, 5-59.
Additional Literature
Righter, K. & Drake, M.J. (2004) Partition coefficients at high pressure and temperature. Treatise on Geochemistry, 2, 425-449.
McIntire, W. L. (1963) Trace element partition coefficients " a review of theory and applications to geology. Geochimica et Cosmochimica Acta, 27, 12, 1209-1264.
Glicksmann, M. E. (2000) Diffusion in solids: Field theory, solid state principles and applications. Wiley, New York, 498 pp.
Crank, J. (1983) Mathematics of diffusion, Oxford University Press, 432 pp.
Manning, J.R. (1968) Diffusion kinetics for atoms in crystals, London, Van Nostrand.
Joestein, R. (1991) Grain boundary diffusion kinetics in silicate and oxide minerals. In: Ganguly, J. (Ed.) Diffusion, atomic ordering and mass transport. Advances in Physical Geochemistry, 8, 345-395, Springer, Berlin.
Ingrin, J. & Blanchard, M. (2006) Diffusion of hydrogen in minerals. Reviews in Mineralogy and Geochemistry, 62, 291-320.
Blundy, J. & Wood, B. (2003) Partitioning of trace elements between crystals and melts. Earth and Planetary Science Letters, 210, 383-397.
Wood, B. & Blundy, J. (2003) Trace element partitioning under crustal and uppermost mantle conditions: the influences of ionic radius, cation charge, pressure and temperature, Treatise On Geochemistry, 2, 9, 395-424.
Related Links
Software to calculate mineral-melt partition coefficients.
Acknowledgements
These materials are being developed with the support of COMPRES, the Consortium for Materials Properties Research in Earth Sciences, under NSF Cooperative Agreement EAR 10-43050 and is partially supported by UNLV's High Pressure Science and Engineering Center, a DOE NNSA Center of Excellence supported under DOE NNSA Cooperative Agreement No. DE FC52-06NA26274.