Phase Equilibria at High Pressure

by Pamela Burnley, University of Nevada Las Vegas

Outline

Introduction

High Pressure Phase Equilibrium Studies

Phase Equilibria Relevant to the Deep Earth

Resources for Learning About Phase Equilibrium

Related Links

Introduction

Studies of phase equilibria are highly relevant to many areas of geosciences because in most cases, mineral systems have the time to reach thermodynamic equilibrium and lack the energy input needed to sustain disequlibrium. With increasing pressure, most crystal structures that are stable at low pressure (e.g. 1 bar) are replaced by denser structures. This has important implications for Earth's interior as well as for the synthesis of novel materials for industrial applications. A significant area of mineral physics research is therefore dedicated towards discovering new phases that may be present either in the deep earth or within other planets and characterizing their physical and chemical properties. Equilibrium relations between phases at high pressure are governed by the same thermodynamic principles that operate at low pressure. There are many good books and resources for brushing up on these concepts including those found elsewhere in the SERC website (see links below). Concepts that are particularly important to understand are: Gibbs Free energy, enthalpy, entropy, chemical activity, Clausius Clapeyron equation, endothermic and exothermic reactions and the phase rule. If one is going to delve into multicomponent systems it is also a good idea to be familiar with Schreinemakers method.

High Pressure Phase Equilibrium Studies

There are a number of different types of high pressure studies related to phase equilibria. There are true phase equilibrium studies that seek to characterize the range of pressure, temperature or chemical activity (e.g. for O₂) over which a given phase (or phase assemblage) is stable. Synthesis studies seek to discover and produce new phases. However, they are distinct from phase equilibrium studies. There are a number of circumstances that can lead to minerals forming outside their thermodynamic stability field. Another major area of interest is phase transformation mechanisms and kinetics.

Reversals: the difference between synthesis and phase equilibrium studies

One of the most important features of a good phase boundary determination is the reversal. A reversal is a pair of experiments where the reactants and products in one experiment become the products and reactants in another experiment. The position of the phase boundary can be said to be somewhere between these bracketing experiments. In-situ experiments (e.g. synchrotron x-ray diffraction) are particularly efficient for conducting phase equilibrium studies because the transformation from one phase assemblage to the other can be run first one way and then back the other at a number of pressure and temperatures during a single experiment.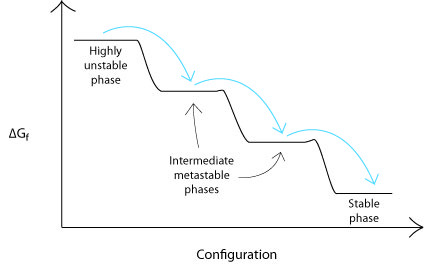 Since phase boundaries are lines (or curves if volatiles are present) at minimum two reversal are required to fully describe a phase boundary. Reversals are necessary for two reasons: 1) Due to kinetics, phases can persist in some cases indefinitely outside of their stability field. Merely witnessing a phase at a given P and T, especially at lower temperatures, does not guarantee that it is the stable phase. 2) As mentioned above, phases can be synthesized outside of their stability field. Some of the reasons that this can occur are related to a phenomena referred to as Ostwald's step rule – which says that the first phase to from in a reaction is not always the one with the lowest free energy but the phase with a free energy closest to the free energy of the reactants. In order to start with a sample that is highly homogeneous, experimentalists may choose a gel or glass; the free energy of these reactants can be quite large. Reactants ground in a mortar and pestle can be highly strained (e.g. Kingma et al., 1993) which can also substantially raise their free energy. So for example, coesite can be produced from highly strained quartz at P and T conditions in the quartz stability field (Green, 1972). For these reasons if one wants to measure the position of a phase boundary or confirm that a given phase in fact has a stability field, reversals are required.

Experimental Concerns

The quality of a phase equilibrium study is highly dependent on how well known P, T and chemical activity are in the experiment. Discussions of uncertainty in P and T can be found in the multi-anvil and diamond anvil pages. Knowing the chemical activity of most elements in an experiment is quite straightforward; if the element was present in the capsule both before and after the experiment its activity is be assumed to be one.

However, there are some important exceptions for elements that are not necessarily trapped in the experiment; this includes volatiles like H₂, H₂O and O₂ as well as elements that participate in solid solutions with sample assembly components abutting the sample (e.g. the capsule or gasket). The state of the art for containing volatiles in solid media apparatus (e.g. the multi-anvil) is to use welded noble metal capsules that are weighed before and after the experiment to guarantee that no mass is lost. However, this strategy may not always be feasible. This is especially true for in-situ experiments where x-ray transparency is required. The use of Au is limited by its melting point and since Fe dissolves in Pt, it cannot be used reliably for working in Fe bearing assemblages. In solid medium experiments if a sample is not sealed in a welded noble metal capsule, the sample assembly exerts a great deal of control on the fugacity of volatiles. Pyrophyllite placed adjacent to the furnace can dehydrate and produce a wet environment, superglue in the hot parts of the assembly can combust and produce an environment that will reduce SiO₂ to Si metal. Graphite furnaces also produce a reducing environment that can destabilize Fe-bearing silicates; wrapping the sample in Fe or Ni foil is usually enough to prevent this. Similar issues occur in the DAC, where the chemical activity in the sample is affected by the confining medium and the gasket. Thus phase equilibrium studies require some thought about the chemical activity of the sample/sample assembly system in order to guarantee that the experiment that is conducted matches the experiment that is envisioned.

Discovery and Synthesis of New Phases

The simplest way to discover a new phase is to put reactants of interest together and bring them to some new pressure temperature condition and either observe them with x-rays at temperature and pressure or quench them and use x-ray diffraction to identify the phases present and search for new phases. However, there are more sophisticated strategies for searching P,T chemistry spaces for new phases. One strategy that has been around for a long time is to use one's knowledge of phase relations in one chemical system to make intelligent guesses about phase relations in another similar chemical system. For example, the observation that Mg₂GeO₄ formed in both an olivine and a denser spinel structured polymorph, led researchers in the 1930's to suggest that (Mg, Fe)₂SiO₄ olivine might also have a spinel structured polymorph which could account for the increase in seismic velocity at ~400 km depth. Many compounds that share the same stoichiometry have phase diagrams that share the same topology. Structures that host elements with larger ionic radii at room pressure often faithfully predict the structures that elements with smaller radii will adopt at high pressure. Another clue that an undiscovered phase is present in a system is if the phase boundary between two phases (e.g. solid and melt) suddenly changes slope. Recently, first principle calculations (e.g. USPEX) have also been used to anticipate the existence of new phases.

Phase Equilibria Relevant to the Deep Earth

Phase diagrams illustrate the stability of phases in Pressure,Temperature, chemical activity space. Many igneous and metamorphic systems contain up to 11 significant chemical components. This means that a full depiction of phase equilibria in these systems requires 13 dimension. Petrologists have devised a host of sections, pseudo sections and projections to create illustrative 2D diagrams from these multi-dimensional spaces. Mineral physics has mostly confined itself to working in relatively simple chemical systems (e.g. MgO-SiO₂) that serve as a proxy for the chemically more complex Earth. Another strategy is to look at changes with pressure and temperature in a single bulk composition (e.g. MORB or pyrolite). A selection of relevant phase diagrams is given below.

A note regarding the names of phases

For conversational convenience, some mineralogists and nearly all mineral physicists use the names of common minerals to refer to other compounds with the same structure. So for example, we use 'spinel' to refer to A₂BO₄ phases that are isostructural with the mineral spinel (MgAl₂O₄) and 'perovskite' to refer to phases that are isostructural with the mineral perovksite (CaTiO₃). Other conventions for naming phases come out of material science and solid state physics. So one commonly sees Greek letters used to refer to polymorphs of a given compound (e.g. α, β, γ, δ, ε). Phases may also be referred to by their packing arrangement; for example BCC for body centered cubic structure, FCC for face centered cubic and HCP for hexagonal close packed. Most high pressure phases were discovered in the lab and bear these sorts of names. However, some have subsequently been identified in meteorites and have been given proper mineral names like Akimotoite and Ringwoodite. This has led to some phases having multiple names (e.g. Ringwoodite = γ-olivine = spinel); which may be somewhat confusing for the uninitiated.

(Mg,Fe)₂SiO₄

(Mg,Fe)₂SiO₄ is a major constituent of the rocky portion of the planet. At low pressure it occurs as the familiar mineral olivine. Most mineralogy texts contain good descriptions of the physical and chemical properties of olivine. The "Orthosilicates" volume of Reviews in Mineralogy (volume 5) provides a comprehensive review. With increases in pressure the olivine structure become unstable relative to Wadsleyite and Ringwoodite which are denser. The transitions in the earth occur at ~410 km and ~520 km. Since this is a two component system, each transition is accompanied by a two phase loop. At ~670 km depth, Ringwoodite disproportionates into a perovskite structured phase (usually just called perovskite) and magnesiowustite (which is sometimes referred to as periclase (the name of the Mg end-member) or in some cases rocksalt (which is the name of the structure)). To simplify life researchers may choose to work in the pure endmember Mg₂SiO₄, (forsterite olivine) or Fe₂SiO₄ (fayalite olivine). A particularly popular starting material for (Mg,Fe)₂SiO₄ is gem quality peridote from San Carlos, AZ which is referred to as San Carlos olivine.

(Mg,Fe)SiO₃

(Mg,Fe)SiO₃ is another major constituent of the mantle. At low pressure it occurs as an orthopyroxene, it converts to clinopyroxene with increasing pressure. Like olivine there are many good resources describing the physics and chemical properties of pyroxenes, the "Pyroxenes" volume of Reviews in Mineralogy (volume 7) is a good place to start. With pressure pyroxenes convert to majorite garnet, or disproportionates to or wadsleyite + stishovite depending on the temperature. These assemblages convert to either the perovskite or illmenite structure (depending on P,T conditions) and finally a relatively newly discovered compound referred to as the post-perovskite structure.
The pyroxene structure can accept a wider range of cations including large cations such at Na, therefore pyroxene is thought to host much of the chemical diversity in the shallow upper mantle. Once it forms, majorite garnet takes on this role. The composition of the mantle is thought to lie somewhere between olivine (Mg₂SiO₄) and pyroxene (MgSiO₃) on the MgO-SiO₂ join. The ratio of olivine to pyroxene is still up for debate, but pyroxene is either the most abundant phase in the shallow upper mantle or the second most abundant. Again there are a plethora of names for the phases in this system. Enstatite is the mineral name for low Ca Mg orthopyroxene. The abbreviation 'OPX' and 'CPX' are often used for ortho- and clinopyroxene. Majorite is usually referred to simply as 'garnet'. Another thing to be aware of is that at low pressure there is an miscibility gap between Fe- and Mg- orthopyroxene and Ca-bearing clinopyroxene (usually referred to by the name of its Mg,Ca- endmember, diopside). So when 'clinopyroxene' is used one must figure out whether the low pressure Ca-bearing variety or the high pressure pyroxene is being referred to.

SiO₂

The low pressure polymorphs of quartz (low and high quartz, cristobalite and tridymite) are familiar to anyone with a geology background since they are common crustal minerals. Coesite occurs less commonly in crustal rocks but is of great interest when it occurs, as it has interesting tectonic implications. Stishovite has the same structure as rutile (TiO₂) and has a mineral name because it is found in meteorite impact sites. At very high pressure stishovite transforms to a CsCl structure and then to one of the structures exhibited by PbO₂; the orthorhombic α-PbO₂ structure. The relative importance of SiO₂ in the deep earth depends on the composition of the lower mantle, which like much things about the deep earth, is still up for debate.

Hydrous Assemblages

The role and mineralogical home of water in the mantle is a topic of great interest and debate. Significant amounts of water may be contained in anhydrous phases but the presence of water may also stabilize a complex series of hydrous phases. The key features to be aware of in mantle phase equilibria dealing with water are 1) the effect of water on the solidous 2) the change from increasing to decreasing temperature stability of hydrous phases with pressure at low to moderate pressure and 3) increasing thermal stability of hydrous phases with pressure above the so called "choke point" at ~5 GPa.

Realistic Mantle Compositions

The composition of the mantle has been modeled as close to the composition of peridotite, as pyrolite (an enriched source which produced basalt and peridotite), as piclogite (with a more Si and Fe rich lower mantle), and as chondrite (the composition of stony meteorites that have not been modified by melting or differentiation). In all cases at least 5 or 6 oxide components are required to describe the system. This vastly complicates phase diagrams because they can no longer be depicted with 2D diagrams without making projections of some sort. Fortunately the broad outline of phase relations in realistic mantle compositions are captured by the phase diagrams for Mg₂SiO₄ and MgSiO₃.

Fe

The core is thought to consist of an Fe-Ni alloy with some mixture of other light elements including S. Phase relations in the pure Fe system are often used as a proxy for phase relations in the core.

Resources for Learning About Phase Equilibria

SERC has an extensive website on Teaching Phase Equilibria which has many tutorial pages suitable for students as well as instructors.

Gibbs Free Energy and Other Thermodynamic Functions

Gibbs Phase Rule: Where it all Begins

Phase Diagrams

Modeling programs (MELTS, TWQ, Perplex, THERMOCALC and Theriak-Domino)

Method of Schreinemakers -- A Geometric Approach to Constructing Phase Diagrams

Other useful sites include:

Thermodynmics and Kinetics from MIT OPEN courseware (readings, lecture notes and videos of lectures) as well as

Tim Grove's Thermodynamics for Geoscientists course which has a focus on the phase equilibria of melts.

References Cited and Additional Literature

Bolfan-Casanova, N., Andrault, D., Amiguet, E. and Guignot, N., 2009. Equation of state and post-stishovite transformation of Al-bearing silica up to 100 GPa and 3000K, Physics of the Earth and Planetary Interiors, 174, 70-77.

Burnley, P. C. and Navrotsky, A., 1996, Synthesis of high-pressure hydrous magnesium silicates: observations and analysis. American Mineralogist. v 81, pp. 317-326.

Fei, Y., and C. M. Bertka, Phase transitions in the Earth's mantle and mantle mineralogy, in Mantle Petrology: Field Observations and High Pressure Experimentation, Y. Fei, C. M. Bertka, and B. O. Mysen, eds., pp. 189-207, Special Publication No. 6, Geochemical Society, Houston, 1999.

Komabayashi, T., and Fei, Y., 2010. Internally consistent thermodynamic database for iron to the Earth's core conditions, Journal of Geophysical Research, 115.

Kung, J., Li, B., Uchida, T., Wang, Y., Neuville, D., and Liebermann, R., 2004. Insitu measurements of sound velocities and densities across the orthopyroxene high-pressure clinopyroxene transition in MgSiO3 at high pressure. Physics of the Earth and Planetary Interiors, 147, 27–44.

Litasov, K., Ohtani, E., Sano, A., Suzuki, A. and Funakoshi, K., 2005. In situ X-ray diffraction study of post-spinel tranformation in a peridotite mantle: Implication for the 660-km discontinuity, Earth and Planetary Science Letters, 238, 311-328.

Liu, L., and Bassett, W.A., Elements, Oxides, and Silicates: High-pressure Phases with Implications for the Earth's Interior. New York: Oxford University Press, 1986.

Murakami, M., and Bass, J.D., 2011. Evidence of denser MgSiO₃ glass above 133 gigapascal (GPa) and implications for remnants of ultradense silicate melt from a deep magma ocean, Proc. Nat. Acad. Sci., 108 (42) 17286-17289.

Murakami, M., Hirose, K., Ono, S., and Ohishi, Y., 2003. Stability of CaCl₂-type and α-PbO₂-type SiO₂ at high pressure and temperature determined by in-situ X-Ray measurements, Geophysical Research Letters, 30(5).

Murakami, M., Hirose, K., Sata, N., and Ohishi, Y., 2005. Post-perovskite phase transition and mineral chemistry in the pyrolitic lowermost mantle, Geophysical Research Letters, 32.

Navrotsky, A., 1989. Silicates and Germanates at High Pressure, Solid State Ionics, 32-33, 288-297.

Ohtani, E., Recent Progress in Experimental mineral Physics: Phase Relations of Hydrous Systems and the Role of Water in Slab Dynamics, in Earth's Deep Mantle: Structure, Composition, and Evolution. Geophysical Monograph Series 160, R.D. van der Hilst, J.D. Bass, J. Matas, and J. Trampert, eds., American Geophysical Union, p 321-334, 2006.

Ulmer, P., and Trommsdorff, V., 1995. Serintine Stability to Mantle Depths and Subduction-Related Magmatism, Science, 268(5212), PP. 858-861.

Acknowledgements

These materials are being developed with the support of COMPRES, the Consortium for Materials Properties Research in Earth Sciences, under NSF Cooperative Agreement EAR 10-43050 and is partially supported by UNLV's High Pressure Science and Engineering Center, a DOE NNSA Center of Excellence supported under DOE NNSA Cooperative Agreement No. DE FC52-06NA26274.