Exponential Equations – Practice Problems
Solving Earth Science Problems with Exponential Growth and Decay
Exponential growth
Problem 1. Cyanobacteria, a group of photosynthetic bacteria, have a rapid growth rate that can lead to quickly proliferating populations. In Earth history, cyanobacteria played an essential role in the increase in oxygen in Earth's atmosphere in the Precambrian, and the organisms are responsible for some algal blooms in lakes.
If a population of cyanobacteria have a growth rate of 0.92 `1/(day)`, how many days will it take for the population to reach 1 billion (1,000,000,000) organisms? Assume the starting population was 5,000 organisms. Remember, the exponential growth equation is
`N=N_0 e^(kt)`
Step 1. Determine which variables are known and unknown
The initial population `(N_0)` is 5,000 organisms and the final population `(N)` is 1,000,000,000 organisms. The growth `(k)` for population growth is `0.92 1/(day)`. In this case, the unknown variable is the length of time (t), so you need to solve for t.
Step 2. Rearrange the equation to isolate the term with the variable you want to solve for.
Divide both sides by
N0
`N/N_0= (N_0 e^(kt))/N_0`
The `N_0` terms on the right side of the equation simplify to 1, and you are left with
`N/N_0= e^(kt)`
Step 3. Use the appropriate logarithm to isolate the variable of interest. Because t is in the exponent, you will need to take the matching base logarithm of both sides to get the unknown isolated.
The base is
e, so we need to take the
natural log (ln) of both sides
`ln(N/N_0)= ln(e^(kt))`
The ln is the inverse function of e, which simplifies our equation to
`ln(N/N_0)= kt`
Divide both sides by k to isolate t
`ln(N/N_0)/k=(kt)/k`
Notice on the right side of the equation, k divided by k simplifies to 1
`(ln(N/N_0))/k=t`
Step 4. Insert known values into the rearranged equation.
`ln((1","000","000","000 "organisms")/(5","000 "organisms"))/(0.92 1/(day))=t`
Step 5. Solve for the unknown.
The units of organisms simplify to 1 and the rate term is in the denominator. When you divide by the rate
`(1/(day))`, you will be left with time in days.
`t=13.3 days`
Problem 2: Determining past population growth and modeling future population growth is important to Earth scientists because society needs to develop plans for resource management, water use, and infrastructure. In 2020, Lagos, Nigeria, one of the fastest growing cities in the world, had a population of 15 million people. If the city continues to grow at rate of 3%, how large will the population be in 2035?
`N=N_0 e^(kt)`
Step 1. Determine which variables are known and unknown
The initial population `(N_0)` is 15,000,000 people. The growth rate `(k)` is 4%, or `0.04 1/(yrs)`, and the time frame `(t)` is 15 years, from 2020 to 2035. For this problem, you need to determine `(N)`, the predicted population in 2035.
Step 2. Rearrange the equation to isolate the term with the variable you want to solve for.
The equation is already arranged to solve for N, so you do not need to rearrange terms.
Step 3. Use the appropriate logarithm to isolate the variable of interest.
Because k and t are both known terms, you do not need to use the natural log and can proceed to step 4.
Step 4. Insert known values into the rearranged equation.
`N=N_0 e^(kt)`
`N=15","000","000 "people" * e^(0.04 1/(yrs)*15 yrs)`
Step 5. Solve for the unknown.
Years divided by years simplify to 1, and you are left with a unitless number in the exponent.
`N=15","000","000 "people" * e^0.60`
`N=27","331","782 "people"`
If you have completed the scientific notation module, you may want to simplify this answer to
`N=27.3xx10^6 "people"`
Hopefully, you can imagine how important long-term planning would be for a city that may nearly double its population in a 15-year period!
Exponential decay
Problem 3: A zircon mineral within a granodiorite originally had 1200 mg of 235U and no 207Pb. It now has 220 mg of 235U. The decay constant, λ, for the 235U/207Pb system is `lambda=9.80xx10^(-10) 1/(yrs)`. Assuming the only chemical process is the radioactive decay of uranium to lead, what is the age of the rock (which is based on the age of the zircon mineral)?
Identify the relevant exponential equation. Because this is about the age of a rock, you will want to use the age equation:
`N=N_0 e^(-lambdat)`
where N is the mass of the isotope present today, N0 is the initial mass of the isotope, t is time, and λ is the decay constant.
Step 1. Determine which variables are known and unknown.
The question gives N0 (1200 mg) and N (220 mg), and λ `(9.80xx10^(-10) 1/(yrs))`. That means the unknown variable is t (time).
Step 2. Rearrange the equation to isolate the term with the variable you want to solve for.
Divide both sides by
`N_0` to simplify the right side of the equation and move
`N_0` to the left side of the equation
`N/N_0=e^(-lambdat)`
Step 3. Use the appropriate logarithm to isolate the variable of interest. Because t is in the exponent, use the matching base logarithm to isolate t.
We want to solve for
t, so we need to take the natural log of both sides because
e is the base term.
`ln(N/N_0)= ln(e^(-lambdat))`
The ln is the inverse function of e, which simplifies our equation to
`ln(N/N_0)=-lambdat`
Divide both sides by -λ to isolate t
`ln(N/N_0)/(-lambda)=(-lambdat)/(-lambda)`
Notice the λ's on the right side of the equation simplify to 1, and you are left with t
`ln(N/N_0)/(-lambda)=t`
Step 4. Insert the known values into the rearranged equation.
`(ln((220 "mg")/(1200 "mg")))/(-9.80xx10^(-10) 1/(yrs))=t`
Step 5. Solve for the unknown.
`(ln((220 "mg")/(1200 "mg")))/(-9.80xx10^(-10) 1/(yrs))=t`
`t=1","731","070","703 "yrs"`
In scientific notation, we would write this as
`t=1.73xx10^9 "yrs"`
You can also use "billions" in the place of "`xx10^9`"
`t=1.73 "billion yrs"`
Problem 4. In some cases, you may know the half-life of a radiogenic isotope, but not the decay rate. Thankfully, you can determine the decay rate from the half-life using the age equation. The half-life (t1/2) for the U-Pb system of 238U/206Pb is 4.47 billion years (4,470,000,000 yrs). Use the age equation below to determine the decay constant for 238U. The half-life (t1/2) and the decay constant (λ) are related by the equation:
`t_(1/2)=ln(2)/lambda`
In this problem, we will use the same steps to determine the decay constant from the age equation
`N=N_0 e^(-lambdat)`
First recognize that we want to solve for the half-life. We don't actually know
N or
N0, but we do know the half-life is the amount of time for half of the radiogenic isotope to decay. This means we can say
`N=N_0/2` and we know the half-life
`(t_(1/2))` is 4.47 billion years.
Step 1. Determine which variables are known and unknown.
Again, we know `N=N_0/2` and we know the half-life `(t_(1/2))` is 4.47 billion years. That means the unknown variable is λ (decay constant).
Step 2. Rearrange the equation to isolate the term with the variable you want to solve for.
Divide both sides by
`N_0` to simplify the right side of the equation and move
`N_0` to the left side of the equation
`N/N_0=e^(-lambdat)`
Step 3. Use the appropriate logarithm to isolate the variable of interest. Because λ is in the exponent, use the matching base logarithm to isolate λ.
We want to solve for λ, so we need to take the natural log of both sides because e is the base term.
`ln(N/N_0)= ln(e^(-lambdat))`
The ln is the inverse function of e, which simplifies our equation to
`ln(N/N_0)=-lambdat`
Divide both sides by -t to isolate λ
`ln(N/N_0)/(-t)=(-lambdat)/(-t)`
Notice the t's on the right side of the equation simplify to 1, and you are left with λ
`ln(N/N_0)/(-t)=lambda`
Step 4. Insert the known values into the rearranged equation.
`ln((N_0/2)/N_0)/(-t)=lambda`
The N0 terms on the left side of the equation simplify to 1, and you are left with
`ln(1/2)/(-t)=lambda`
Importantly, the `ln(1/2)=-ln2`, which simplifies the equation further to the equation at the beginning of this problem
`ln(2)/(t_(1/2))=lambda`
The `1/2` added as a subscript to t is to show it represents the half-life
Step 5. Solve for the unknown.
`ln(2)/(4","470","000","000 yrs)=lambda`
`t_(1/2)=0.000000000155 1/(yrs)`
`t_(1/2)=1.55xx10^-10 1/(yrs)`
Problem 5. Atmospheric pressure and altitude have an exponential decay relationship describe the barometric equation:
`P=P_0*e^(-z/H)`
where P is the atmospheric pressure at a given altitude; P0 is the atmospheric pressure at sea level; z is the altitude above sea level; and H is the scale height of the atmosphere, which is the vertical distance pressure decreases by a factor of e (2.718). Using this equation, estimate the atmospheric pressure at an altitude of 4,000 meters (m) above sea level. Assume the atmospheric pressure at sea level is 1013 millibars (mb) and the scale height of the atmosphere is 8,000 m.
Step 1. Determine which variables are known and unknown.
You want to determine the pressure at a given altitude (P), so that is the unknown variable.
Step 2. Rearrange the equation to isolate the term with the variable you want to solve for.
For this problem, the equation is already arranged properly.
`P=P_0*e^(-z/H)`
Step 3. Use the appropriate logarithm to isolate the variable of interest. Because P is not in the exponent and the terms in the exponents are given, you can insert the known values into the equation
`P=1013 mb *e^((-4000 m)/(8000 m))`
Step 4. Solve for the unknown.
Notice how the units of meters (m) simplify to 1, and you are left with millibars (mb).
`P=1013 mb *e^((-4000 "m")/(8000 "m"))`
The remaining exponent is a unitless number because m divided m simplifies to 1
`P=1013 mb *e^(-0.5)`
`P=1013 mb *0.607`
`P=614.4 mb`
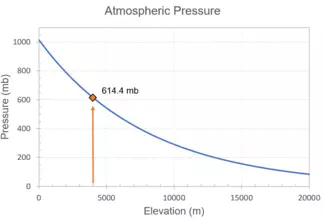
Use the graph of atmospheric pressure vs. elevation to check your answer. Is your answer consistent with the exponential decay curve on the graph?
You will see that the decay curve crosses the elevation of 4000 m at approximately 614 mb. This example highlights that you can calculate the value using an equation or estimate the same value if you have a graph that displays the relationship.

Problem 6. Ground Penetrating Radar (GPR) is commonly used in geophysical surveys to investigate subsurface features. The attenuation of GPR signals as they penetrate the ground can be modeled using an exponential decay equation:
`A=A_0*e^(-kd)`
where A is the decreased amplitude of the GPR signal; A0 is the initial amplitude of the GPR signal; k is the attenuation coefficient; and d is the depth.
Imagine you were tasked with conducting a GPR study in central Minnesota to determine the depth to unmarked utility lines. Your field site is in clay-rich soil that has high conductivity, which means the attenuation coefficient (k) is high. For this clay-rich soil k is `0.4 1/m`. If the initial amplitude was 4000 volts per meter `(V/m)`, at what depth will the amplitude be reduced by 50%?
Step 1. Determine which variables are known and unknown.
The question gives A0 as `4000 V/m` and says 50% amplitude reduction, which means A is `2000 V/m`, and k is `0.4 1/m`. The unknown variable is d (depth).
Step 2. Rearrange the equation to isolate the term with the variable you want to solve for.
`A=A_0 e^(-kd)`
Divide both sides by `A_0`
`A/A_0=e^(-kd)`
Step 3. Use the appropriate logarithm to isolate the variable of interest. Because d is in the exponent, use the matching base logarithm to isolate d.
You want to solve for
d, so we need to take the natural log of both sides because
e is the base term.
`ln(A/A_0)= ln(e^(-kd))`
The ln is the inverse function of e, which simplifies our equation to
`ln(A/A_0)=-kd`
Divide both sides by -k to isolate d
`ln(A/A_0)/(-k)=(-kd)/(-k)`
Notice the k's on the right side of the equation divide by each other and simplify to 1
`ln(A/A_0)/(-k)=d`
Step 4. Insert the known values into the rearranged equation.
`(ln((2000 V/m)/(4000 V/m)))/(-0.4 1/m)=d`
Step 5. Solve for the unknown.
`(ln((2000 V/m)/(4000 V/m)))/(-0.4 1/m)=d`
`d=1.73 m`
Next steps
TAKE THE QUIZ!!
I think I'm competent with exponential equations and I am ready to take the quiz! This link takes you to WAMAP. If your instructor has not given you instructions about WAMAP, you may not have to take the quiz.Or you can go back to the Exponential Equations explanation page.