System Identification and LQR Controller for Propeller Operated Balancing Beam (Bi-Copter)

Eniko Enikov, The University of Arizona,

Author Profile
Initial Publication Date: October 7, 2025

Summary

This laboratory experience illustrates the complete cycle of feedback controller design by extracting a linear model of an open-loop system, designing a controller, and testing the closed-loop response. Students have the opportunity to test different models using the System Identification Toolbox and design controllers using the Control Systems Toolbox. The experiment is implemented in hardware using an Arduino Nano IOT board and as a digital twin operating in a Simulink/Simscape environment. A step-by-step Live Script guides the users through the experimentation.

Share your modifications and improvements to this activity through the Community Contribution Tool »

Learning Goals

This activity can be used with both undergraduate and graduate students.

Upon completion, undergraduate students should be able to:

  • Identify transfer functions from experimental data
  • Tune PID controllers using MATLAB pidtune() command or PIDTunner app.
  • Test closed-loop response with the designed PID controller 

Upon completion, graduate students should be able to:

  • Identify transfer functions from experimental data
  • Identify state-space models of arbitrary order using MATLAB n4sid() command
  • Analyze the residual error using MATLAB resid() command
  • Design a servo controller containing an integrator using polynomial algebra using MATLAB toeplitz() command
  • Design servo controller containing an integrator using discrete-time linear quadratic regulator (LQR) theory and MATLAB dlqr() command

Context for Use

The module is intended for senior-year undergraduate students enrolled in their fist course on controls, or for Master-level graduate students learning state-space description and state-space design methods. Users should be familiar with basic MATLAB commands and commands from Control Systems Toolbox (tf, ss, step, feedback, dlqr, acker) and System Identification (iddinput,iddata, tfest, arx, n4sid) toolboxes.

The available Live Script and open- and closed-loop Simulink models enable users to automatically implement activities by simply running the Live Script. Undergraduate students can use the closed-loop PID Simulink model to test their PID controller.

More advanced users can modify the demonstration files and carry out independent experiments.

Description and Teaching Materials

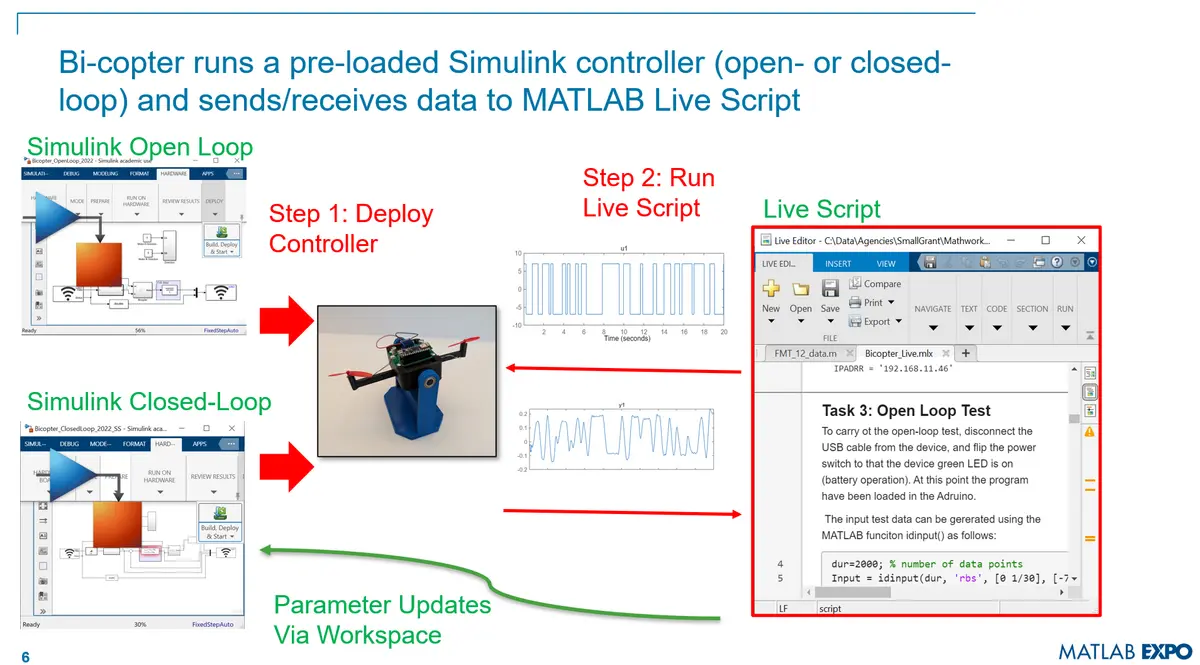
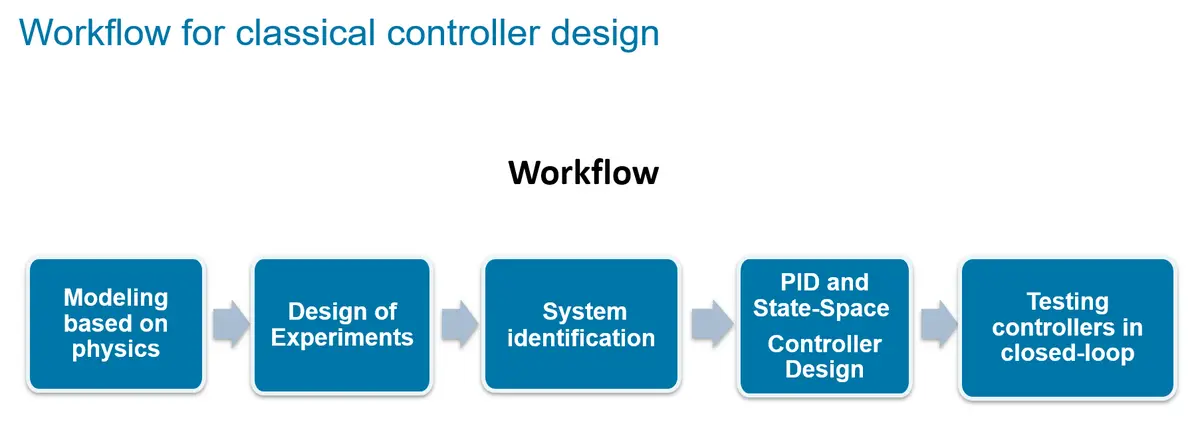
A detailed description of the experiments, along with all necessary files to replicate them at any institution, is available online using the GitHub repository. A typical workflow includes running open-loop test, extracting a model, designing a controller, and testing the controller.

Open and closed-loop tests are initiated from the MATLAb LiveScript, after deploying the open- and closed-loop simulink models in the Bi-Copter's Arduino controller.

Further details are available in our presentation (see link below).

final_Hands-On Learning with the Low-Cost Bi-Copter From Fundamentals to Advanced Controls.pdf (Acrobat (PDF) 6.5MB Oct28 25).


Teaching Notes and Tips

Areas where students need help or some guidance include:

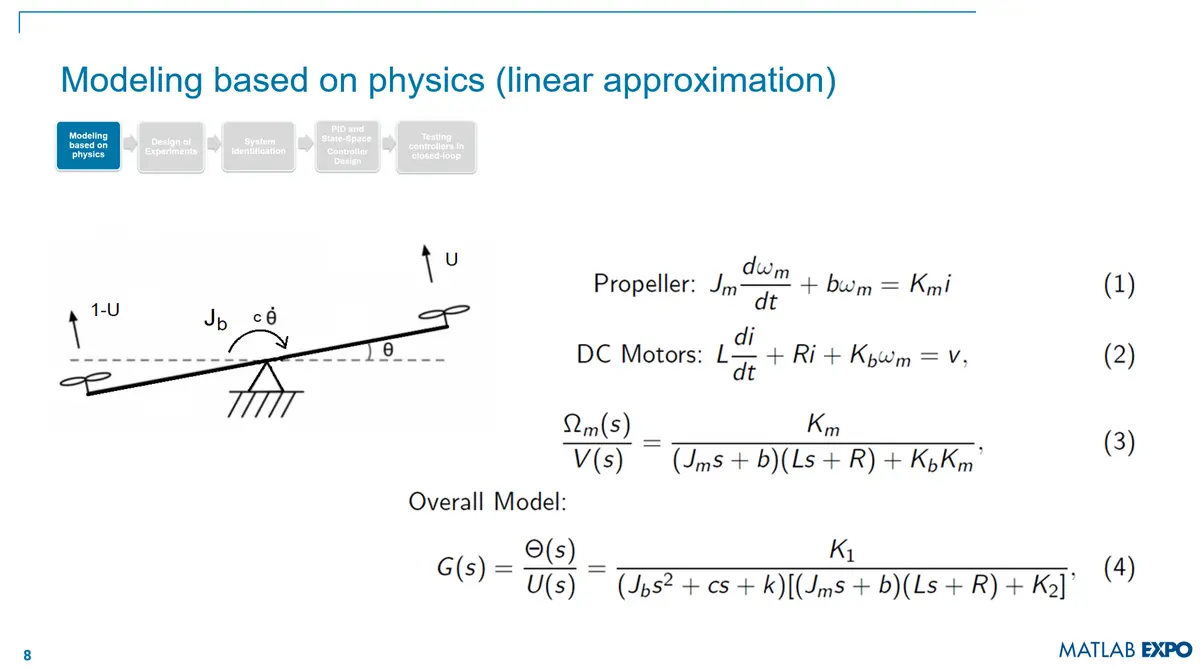
  • Choosing the order of the model. One approach is to present different independent energy storing components (modes), leading to a 4th or 6th order models.

  • Selecting the bandwidth and amplitude of the excitation input during open-loop testing in order to obtain a good model estimation

    Input = idinput(dur, 'rbs', [0 1/30], [-7 7]);
  • Guidance in selecting the gain cross-over frequency, if PIDtune uses the frequency design method. 

 C0 = pid(1,1,1,'Ts',ts,'IFormula','BackwardEuler','DFormula','BackwardEuler');
C=pidtune(G,C0,1.5)  


Assessment

Undergraduate students' assessment:

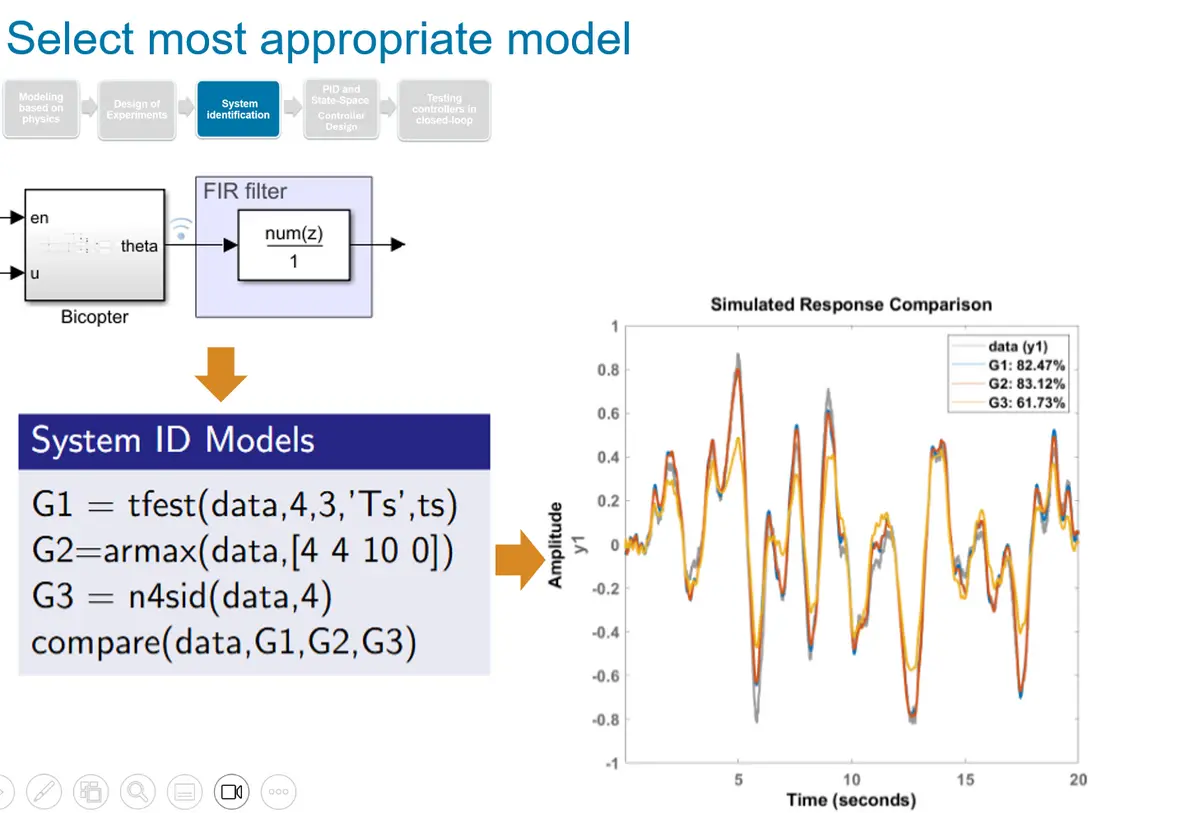
  • Students must achieve a model that agrees at least 75%. G3 below is a failed example

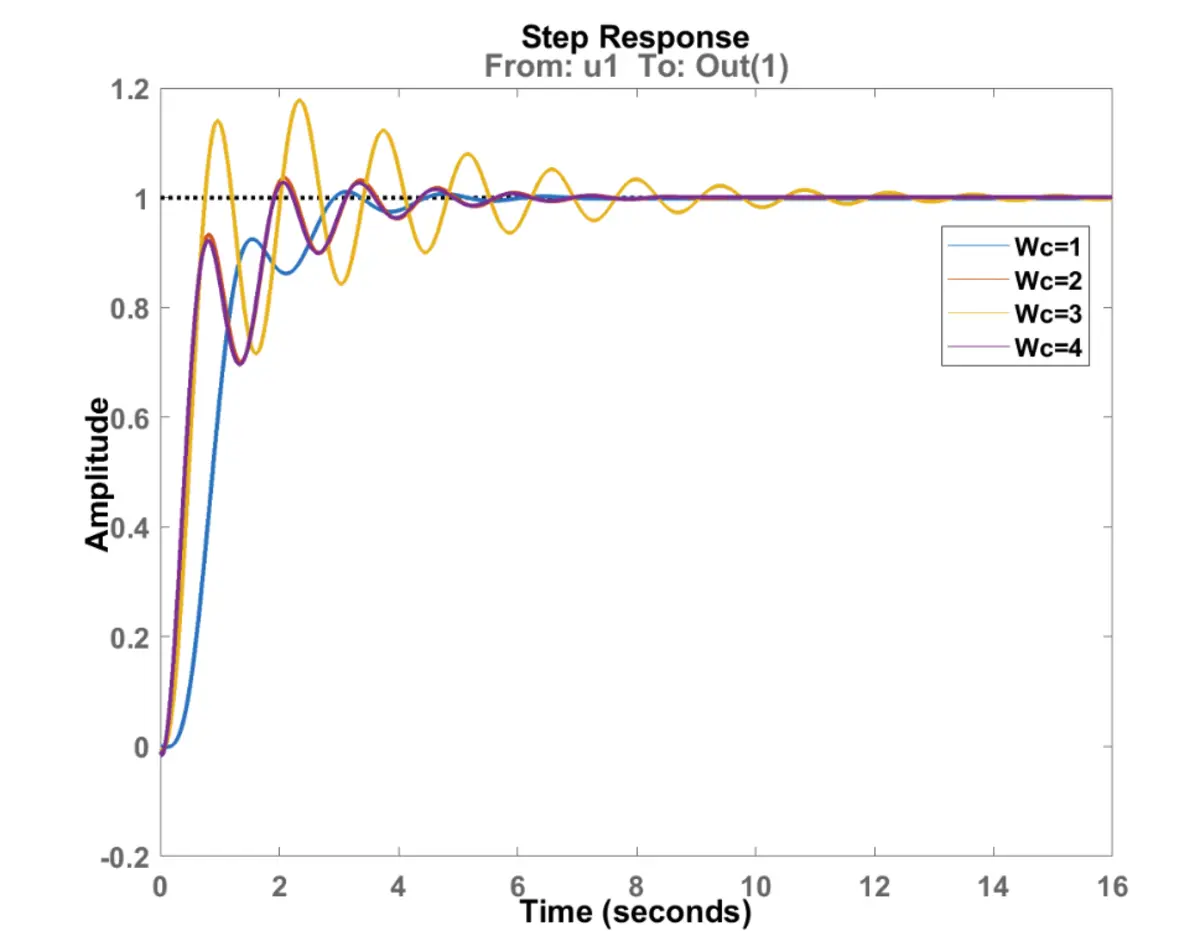
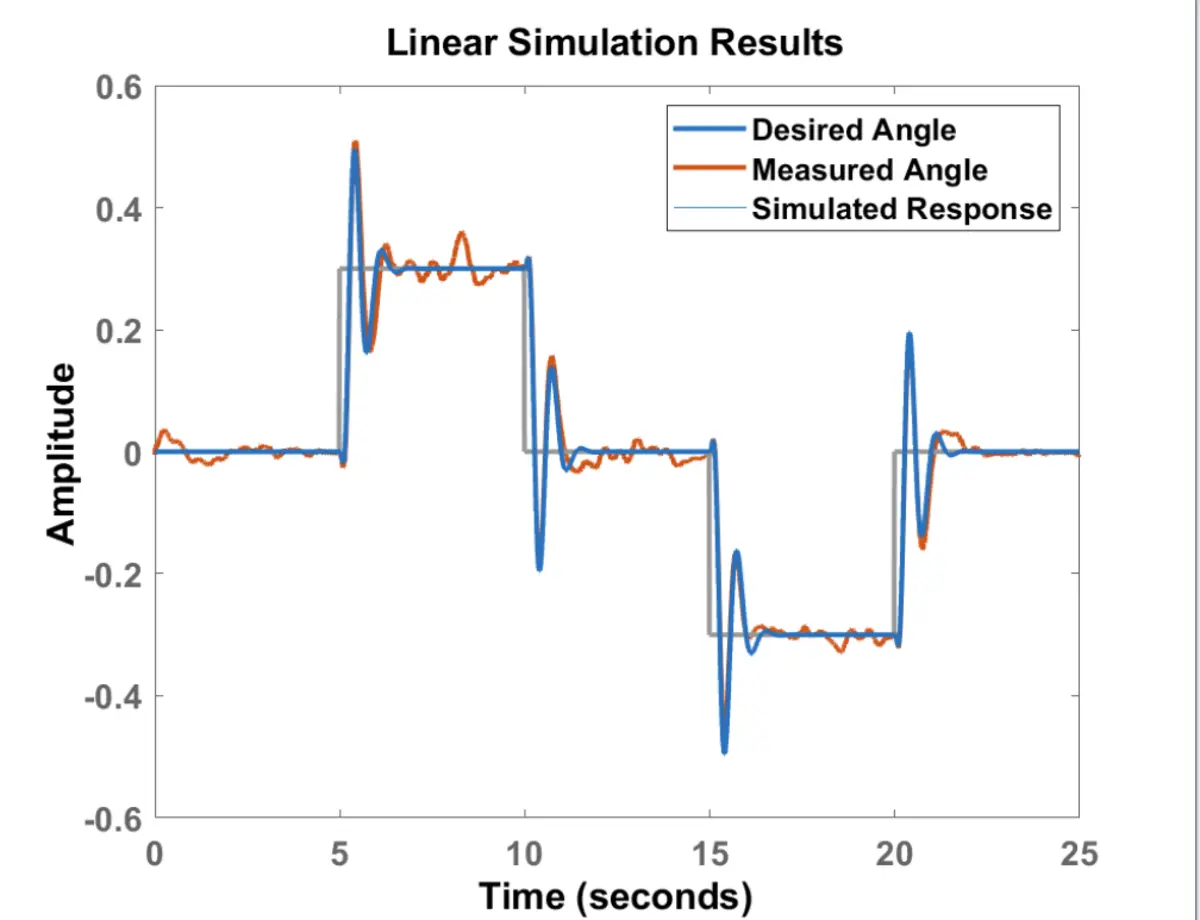
  • Students must demonstrate a step response that is stable with zero steady-state error. In the example below all designs are acceptable

  • Students must demonstrate successful tracking of reference input with zero steady-state error. The plot below shows a correct response.

Graduate students' assessment includes:

  • All of the above
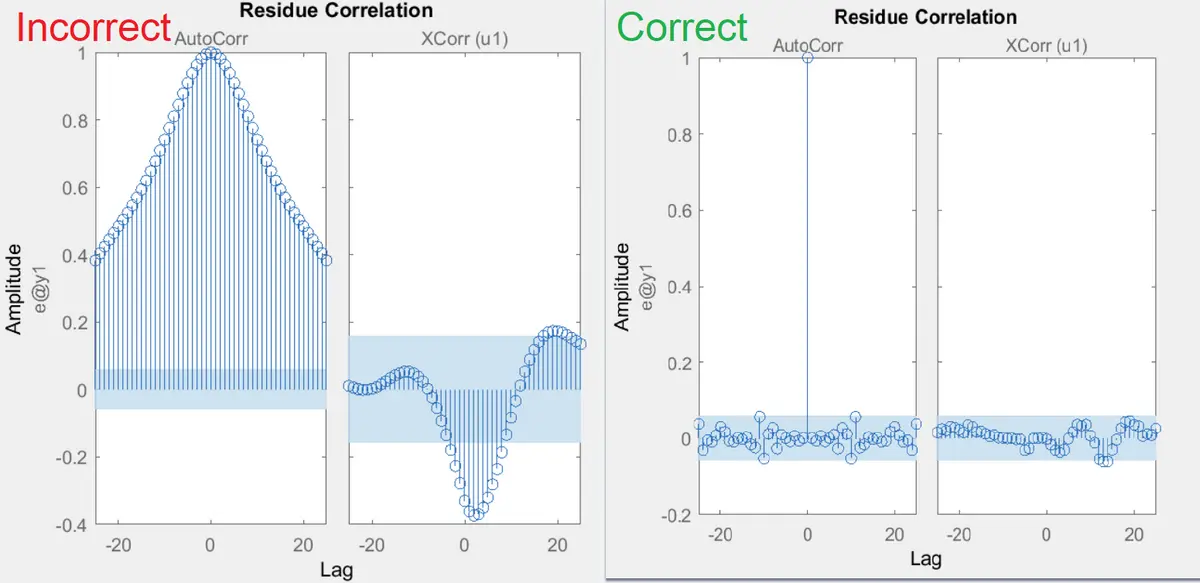
  • Analysis of the residual error of the system identification experiments

  • Report a controller transfer function using direct polynomial method
  • Report a controller transfer function using the LQR method

References and Resources