Students should learn

- how the concept of iteration can be applied to simulating a time-series physical process
- how the concept of conditional logic can be applied to simulate a state-variant physical process

MATLAB is used as a general purpose programming environment, but any high-level general purpose programming environment could be used. The programming environment provides a mechanism to implement a simulation of a physical process so that students can predict a time-varying state from initial values.

Depending on the level of scaffolding, students will need to engage with the following higher-order thinking skills

- synthesizing the concept of friction with an iterative simulation
- determining a logical state-based test for "is an object moving"
- applying Euler's method for iteratively solving an ODE
- this particular course does not introduce the concepts of or expect knowledge of Eulers method, or ODEs. We provide constant acceleration equations to students and tell them to treat each time slice as a single constant acceleration calculation.

This is a first year (university) introductory engineering course offered at a large public research institution. The course is consists both a lecture and lab component, the lectures are run under a flipped-classroom model and the labs are run by GTAs

A block with weight W is at rest on a surface. A time varying pull force P is applied at and angle of θ.

×

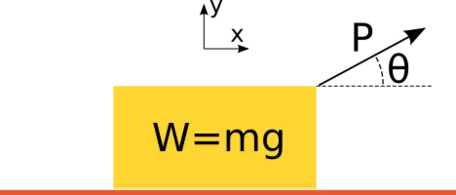
Given

• time, an array of time values in seconds
• pullForce, an array of force values in Newtons
• theta, a scalar angle in degrees CCW from the horizontal axis
• u_k, the coefficient of kinetic friction between the block and surface
• u_s, the coefficient of static friction between the block and surface
• weight, the weight of the block in Newtons
• g, the acceleration due to gravity in m/s^2

Task

Calculate the acceleration and velocity of the block at each value of time.

Output

Always print the velocity value at 3 and 5 seconds.

If the final velocity value is greater than zero

• print the final time and velocity value
• otherwise, print the time at which velocity returned to rest

No other output should be printed to the command window!

• Format all velocity values to exactly 3 significant figures.
• Format all the time at which the block returns to reset to exactly 2 decimal places

Sample output when the final velocity is zero:

Velocity at 3 seconds is 7.95 m/s
Velocity at 5 seconds is 6.94 m/s
The block returns to rest at 6.76 seconds

Sample output when the final velocity is greater than zero:

Velocity at 3 seconds is 8.92 m/s
Velocity at 5 seconds is 9.49 m/s
Velocity at 8 seconds is 0.664 m/s

Hints

Don't Know Where to Start?

• the examples on the "Accumulate Patter" page implement the basic structure that will be used for the calculations here.

start with implementing the velocity equation and work backwards:

$v\_n = v\_{n-1} + a\_n\,\Delta{t}$

Now that it is implemented as MATLAB code, we need to make sure all the necessary parts are available:

• is $v_{n-1}​ available? if not, what can you do to make it available?
• is $a_n$​ available? if not, implement it. The exact formula comes from your FBD=KD

Calculate

• You may assume that the time delta \Delta{t}Δt is uniform for all time. Do not assume its value, still calculate it from the give time variable, but you may keep just a scalar value rather than an array.

There are several ways to determine when to use a previous iteration's values and when to use a current iteration's values in calculations. One way is not necessary "correct", but differences will result in slightly different results. The reference implementation as well as numeric check is using the following approach:

• Assign initial values before the loop starts, start the loop iteration variable at 2
• Determine whether the object is moving or not as the first calculation in the loop body. Since it is the first calculation we use values from the previous iteration for this determination.
• Calculate all force and acceleration values, including friction forces, using the current iteration's values
• Calculate the current acceleration from the current force values.

Calculate the current value of velocity last. Accumulate the previous velocity value with the current acceleration and time delta.

$v_{n} = v_{n-1} + a_{n}\Delta{t}$

• define a variable moving that is a logical (true/false) and is TRUE when the block is moving.
• The block is moving when velocity is greater than zero OR the horizontal pull force is greater than F_{max}Fmax​. Since this is one of the first calculations in the loop, use values from the previous iteration to determine this value.
  
  
   

This could be paired with a measurement activity where students measure coefficients of friction, record a physical lab of a block being pushed/pulled or sliding down a surface, and then comparing measured data with predicted results followed by a reflection of why the two differ.

Completed source code is submitted. The instructor may either

1. Review for correctness and provide feedback without running the code, e.g. if the primary learning objective is describing a physical process as an algorithm, but not necessarily producing working code
2. Run the code, check for errors, review the output etc. and provide feedback, e.g. if a primary learning objective is producing working code
3. A combination of 1 and 2