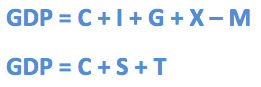Solving Simultaneous Equations

Introduction

Economic models often use a system of equations. When the same variables appear in more than one equation, they often all need to be solved at the same time --- that is simultaneously.

As long as we have the same number of equations as unknown variables --- for example two equations and two unknown variables --- we can solve these equations using a simple set of steps.

An example

×

Provenance: Jeffrey Sarbaum, University of North Carolina at Greensboro
Reuse: This item is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license http://creativecommons.org/licenses/by-nc-sa/3.0/ You may reuse this item for non-commercial purposes as long as you provide attribution and offer any derivative works under a similar license.

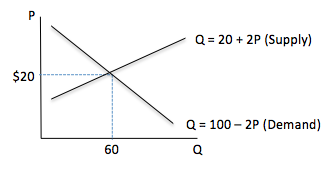
The familiar supply and demand is a model, predicting what happens to prices and quantities. If the market moves toward an equilibrium, then we can predict prices and quantities by solving simultaneous equations for supply and demand. We'll solve one of these below.

Steps for solving simultaneous equations

This page will show you how to solve simultaneous equations using:

• the substitution method or
• the elimination method

Both methods give us the same answer. For each problem, choose the one that is most straightforward.

The Substitution Method

Here are the steps for solving simultaneous equations using the substitution method. The equation is for market equilibrium, a common model in both macroeconomics and microeconomics.

1. Read both equations and identify the unknown variables.
   
   
   Show an example using supply and demand
   Hide

   an example using supply and demand

   $2Q = 100 - 2P \text{ (Demand)}$
   
   $3Q = 20 + 2P \text{ (Supply)}$
   
   The unknown variables in both equations are Q (quantity) and P (price).
   
   
2. Pick an equation and isolate one of its variables. That is, rearrange this equation so that the variable you selected is by itself on the lefthand side of the equals sign. Be sure to follow the rules for rearranging equations and simplify as much as possible. You now have an equation for the variable you chose, defined in terms of the other variable.
   
   
   Show continuing our example using supply and demand
   Hide

   continuing our example using supply and demand

   Let's choose the equation Q = 100 – 2P and solve it for P one step at a time.
   
   

   1. Add 2P to both sides.
      
      $2Q \color{red}{+ 2P} = 100 – 2P \color{red}{+ 2P}$
      
   2. Cancel out the 2P's on the right hand side.
      
      $\require{cancel}2Q + 2P = 100 \cancel{- 2P + 2P}$
      
      $2Q + 2P = 100$
      
   3. Subtract 2Q from both sides.
      
      $2Q + 2P \color{red}{- 2Q} = 100 \color{red}{- 2Q}$
      
   4. Cancel out the Q's on the left hand side.
      
      $\cancel{2Q} + 2P \cancel{- 2Q} = 100 – 2Q$
      
      $2P = 100 - 2Q$
      
   5. Divide both sides by 2.
      
      $2P\color{red}{/2} = (100 – 2Q)\color{red}{/2}$
      
   6. Cancel out the 2's on the left hand side and simplify.
      
      $\cancel{2}P/\cancel{2} = (100 - 2Q)/2$
      
      $P = (100 - 2Q)/2$
      
      $P = 100/2 - 2Q/2$
      
      $P = 50 - Q$
      

   Now we have a new equation for P in terms of Q.
   
   
3. Substitute this new equation for the variable in the other equation and simplify. When you're done with this step you will have a value for the variable you did not pick in Step #2.
   
   
   Show continuing our example using supply and demand
   Hide

   continuing our example using supply and demand

   Our new arrangement of the first equation isolates the variable P. Therefore, we want to replace the variable P in the second equation with this new equation.
   
   Our second equation is 3Q = 20 + 2P. We want to find the value of Q.
   
   

   1. Substitute in P = 50 - Q and simplify.
      
      $3Q = 20 + 2(50 - Q)$
      
      $3Q = 20 + 2(50) - 2(Q)$
      
      $3Q = 20 + 100 - 2Q$
      
      $3Q = 120 - 2Q$
      
   2. Add 2Q to both sides of the equation.
      
      $3Q \color{red}{+2Q} = 120 - 2Q \color{red}{+ 2Q}$
      
   3. Cancel out the Q's on the right hand side and simplify.
      
      $3Q + 2Q = 120 \cancel{- 2Q + 2Q}$
      
      $5Q = 120$
      
   4. Divide both sides by 5.
      
      $5Q\color{red}{/5} = 120\color{red}{/5}$
      
   5. Cancel out the 5's on the left hand side and simplify.
      
      $\cancel{5}Q/\cancel{5} = 120/5$
      
      $Q = 24$
      

   We now have a value for the variable Q.
   
   
4. Take the equation you derived in Step #2, plug in the value you found in Step #3, and simplify. When you're done, you will have a value for the variable you selected in Step #2.
   
   
   Show continuing our example using supply and demand
   Hide

   continuing our example using supply and demand

   Plug Q = 24 into P = 50 - Q and simplify.
   
   $P = 50 – (24)$
   
   $P = 26$
   
   We now have a value for the variable P.
   
   
5. Plug the values you found for both variables back into each equation and verify that the equations both hold true.
   
   
   Show the conclusion of our supply and demand example
   Hide

   the conclusion of our supply and demand example

   Plug in Q = 24 and P = 26 into 2Q = 100 - 2P and simplify.
   
   $2(24) = 100 - 2(26)$
   
   $48 = 100 - 52$
   
   $48 = 48$
   
   Verified: This equation holds true for the values Q = 24 and P = 26
   
   Plug in Q = 24 and P = 26 into 3Q = 20 + 2P and simplify.
   
   $3(24) = 20 + 2(26)$
   
   $72 = 20 + 52$
   
   $72 = 72$
   
   Verified: This equation also holds true for the values Q = 24 and P = 26.
   
   

The Elimination Method

Now let's see how the elimination method works to solve for market equilibrium given linear supply and demand functions.

1. Read both equations and identify the unknown variables.
   
   
   Show an example using supply and demand
   Hide

   an example using supply and demand

   $2Q = 100 - 2P \text{ (Demand)}$
   
   $3Q = 20 + 2P \text{ (Supply)}$
   
   The unknown variables in both equations are Q (quantity) and P (price).
   
   
2. Choose the variable you want to eliminate first, and compare the signs and magnitudes of the coefficients on this variable in both equations.
   
   If the coefficients are the same magnitude and the opposite sign, add the equations and then solve for the remaining variable.
   
   
   If the coefficients are the same magnitude and the same sign:
   
   

   Subtract the equations and then solve for the remaining variable.

   If the coefficients are not the same magnitude:
   
   

   Use multiplication and/or division to get the magnitudes equal and opposite in sign. Then, add the equations and solve for the remaining variable.

   Show When coefficients of the same magnitude and opposite sign
   Hide

   When coefficients of the same magnitude and opposite sign

   $2Q = 100 - 2P \text{ (Demand)}$
   
   $3Q = 20 + 2P \text{ (Supply)}$
   
   The coefficients on the variable P are of the same magnitude (2), but with opposite signs. Thus, we will add these two equations and then solve for Q.
   
   $2Q = 100 - 2P$ $+ 3Q = 20 + 2P$
   
   $2Q = 100 - \cancel{2P}$ $+ 3Q = 20 + \cancel{2P}$
   
   $5Q = 120$
   
   $5Q\color{red}{/5}= 120\color{red}{/5}$
   
   $\cancel{5}Q/\cancel{5}= 120/5$
   
   $Q = 24$
   
   
3. Plug the value you got from step #3 into one of your equations and solve for the other variable.
   
   
   Show Solving for the other variable
   Hide

   Solving for the other variable

   1. Plug Q = 24 into 2Q = 100 - 2P.
      
      $2(24)= 100 - 2P$
      
      $48 = 100 - 2P$
      
   2. Add 2P to both sides.
      
      $48 \color{red}{+ 2P} = 100 - 2P \color{red}{+ 2P}$
      
   3. Cancel out the 2P's on the right hand side.
      
      $48 + 2P = 100 \cancel{- 2P + 2P}$
      
      $48 + 2P = 100$
      
   4. Subtract 48 from both sides.
      
      $48 + 2P \color{red}{ - 48} = 100 \color{red}{ - 48}$
      
   5. Cancel out the 48's on the left hand side and simplify.
      
      $ \cancel{48} + 2P \cancel{- 48} = 100 - 48$
      
      $2P = 52$
      
   6. Divide both sides by 2.
      
      $2P\color{red}{/2} = 52\color{red}{/2}$
      
   7. Cancel out the 2's on the left hand side and simplify.
      
      $\cancel{2}P/\cancel{2} = 52/2$
      
      $P = 26$
      
4. Plug the values you found for both variables back into each equation and verify that the equations both hold true.
   
   
   Show Verifying your solution
   Hide

   Verifying your solution

   Plug in Q = 24 and P = 26 into 2Q = 100 - 2P and simplify.
   
   $2 (24) = 100 - 2(26)$
   
   $48 = 100 - 52$
   
   $48 = 48$
   
   Verified: The first equation holds true for the values Q = 24 and P = 26.
   
   Let's try the other equation. Plug in Q = 24 and P = 26 into 3Q = 20 + 2P and simplify.
   
   $3(24) = 20 + 2(26)$
   
   $72 = 20 + 52$
   
   $72 = 72$
   
   Verified: The second equation also holds true for the values Q = 24 and P = 26.
   
   

Solving simultaneous equations in Macroeconomics

Solving simultaneous equations are used in many macroeconomic models.

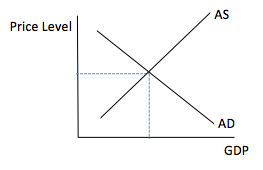
• The aggregate supply/aggregate demand (AS/AD) model requires two equations. Given equations for aggregate demand and aggregate supply, we can solve this system of equations to determine the equilibrium price level and the equilibrium level of output.
  
  
  

  ×

  

  Provenance: Jeffrey Sarbaum, University of North Carolina at Greensboro
  Reuse: This item is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license http://creativecommons.org/licenses/by-nc-sa/3.0/ You may reuse this item for non-commercial purposes as long as you provide attribution and offer any derivative works under a similar license.
  
  
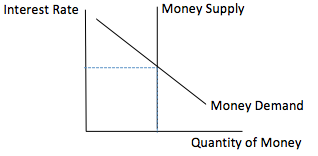
• The demand and supply for money shows the impact of interest rates on the quantity of money. Given equations for money demand and money supply, economists can show the interest rate at which the money market is in equilibrium.
  
  
  

  ×

  

  Provenance: Jeffrey Sarbaum, University of North Carolina at Greensboro
  Reuse: This item is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license http://creativecommons.org/licenses/by-nc-sa/3.0/ You may reuse this item for non-commercial purposes as long as you provide attribution and offer any derivative works under a similar license.
  
  
• The Income-Expenditure model requires two equations. One shows the impact of total national income on national spending. The other equations indicates where the planned total spending will equal total income. Solving these two equations simultaneously shows the predicted equilibrium income.
  
  
  

  ×

  

  Provenance: Jeffrey Sarbaum, University of North Carolina at Greensboro
  Reuse: This item is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license http://creativecommons.org/licenses/by-nc-sa/3.0/ You may reuse this item for non-commercial purposes as long as you provide attribution and offer any derivative works under a similar license.
  
  

Solving simultaneous equations in Microeconomics

In microeconomics simultaneous equations are used in models of market equilibrium, models of firm production and models of consumer behavior. Solving these equations helps economists can predict prices and quantities.

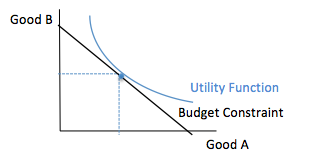
• In the model of consumer choice (here, applied to utility maximization), equations describe consumer preferences for a set of goods and services subject to budget restraint. Solving these simultaneous equations predicts consumer behavior.
  
  
  

  ×

  

  Provenance: Jeffrey Sarbaum, University of North Carolina at Greensboro
  Reuse: This item is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license http://creativecommons.org/licenses/by-nc-sa/3.0/ You may reuse this item for non-commercial purposes as long as you provide attribution and offer any derivative works under a similar license.
  
  
• Models of cost minimization for business firms use simultaneous equations to describe production possibilities and cost constraints. Solving these simultaneous equations indicates a firm's cost minimization for different output levels.
  
  
  

  ×

  

  Provenance: Jeffrey Sarbaum, University of North Carolina at Greensboro
  Reuse: This item is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license http://creativecommons.org/licenses/by-nc-sa/3.0/ You may reuse this item for non-commercial purposes as long as you provide attribution and offer any derivative works under a similar license.