What are Model-Eliciting Activities?

Model-eliciting activities (MEAs) are activities that encourage students to invent and test models. They are posed as open-ended problems that are designed to challenge students to build models in order to solve complex, real-world problems. The six essential principles of MEAs are listed at the end of this section. They may be used to engage the students in statistical reasoning and thinking and provide a means for statistics teachers and researchers to better understand students' thinking.

MEAs are created to look like authentic, real-world statistical problems and require students to work in teams of 3-4 students. The teams generate solutions to a problem via written descriptions, explanations and constructions by "repeatedly revealing, testing, and refining or extending their ways of thinking" (Lesh, Hoover, Hole, Kelly, & Post, 2000, p. 597). In this way, MEAs are thought-revealing as the students' products provide windows into the thinking processes they used to develop the solutions.

While many statistics instructors, particularly at the introductory level, use one or more traditional types of student activities in their classes, these activities are typically quite different than MEAs (see Table 1 below). Activities may also be used to engage students in statistical reasoning and thinking, but they are typically used for a different purpose than a MEA. We think that both MEAs and more traditional types of statistical activities can be used as part of a statistics class.

Some differences between MEAs and other types of typical in-class statistical activities are shown in Table 1. It is important to note that MEAs are not used instead of other types of in-class activities, but that both can be used effectively in a course, but to serve different purposes.

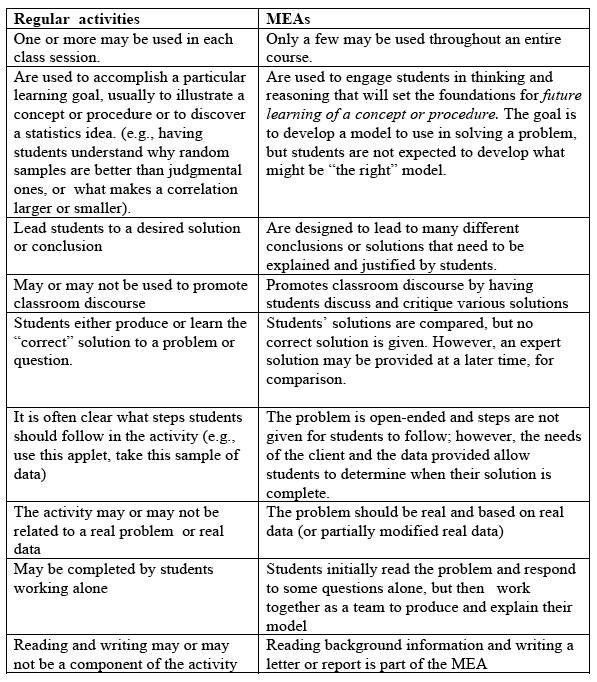Table 1: Comparison of MEA to other typical in-class activities used to teach statistics

Six Principles for Model-Eliciting Activities

The six essential principles for MEAs (Lesh, et al., 2000) are described below:

1. Model Construction Principle: Problems must be designed to allow for the creation of a model dealing with:

• Elements
  
• Relationships and operations between these elements
  
• Patterns and rules governing these relationships
  

In order for the MEA to be thought-revealing, the MEA can require:

• An explicit construction
• Description
• Explanation
• Justified prediction

MEAs have students:

• Quantify (e.g., show how well a model works)
• Coordinate information and relationships
• Make predictions (apply the model to a new problem or data set)
• Identify a pattern or trend.

The final product is a model that:

• Has elements
• Defines relationships among the elements
• Defines operations for how elements interact
• Identifies patterns or rules that apply to the relationships and operations.

2. The Reality Principle: Problems must be meaningful and relevant to the students and be based on real or slightly modified real data. The solution should be "real" and meaningful in the students' everyday lives. Therefore, the context of the situation should:

• Identify the audience who will use or be served by the solution.
• State the purpose of the solution for the audience.
• State why the audience needs the solution.
• State a problem that makes sense in terms of real life knowledge and experience

This can be established through a set of preparatory questions that set a (statistical) focus for reading introductory articles and other information. The preparatory questions can also form the basis for whole class or small group discussions of the articles.

3. Self-Assessment Principle: Students must be able to self-assess or measure the usefulness of their solutions. The problem statement must strongly suggest appropriate criteria for assessing the usefulness of a solution. The data must also play a part in allowing students to self-assess. These criteria should promote selection, refinement, and elaboration of models. In order to do this, the problem statement must:

• State a clear purpose
• Require self-assessment and a need for improvement
• Clearly state when a solution is achieved (through clear criteria)

To make progress, students must be able to:

• Detect deficiencies in the current conceptualization
• Compare alternatives and select the most promising ones
• Integrate the strengths among the alternatives, minimize weaknesses
• Extend and refine promising alternatives
• Assess adaptations

One mechanism for delivering these criteria and the motivation for self-assessment and refinement is to establish a "client" who is making the request and specifies the parameters.

4. Model Documentation Principle: Students must be able to reveal and document their thinking processes within their solution. Students responses must produce an audit trail by revealing the:

• Givens (their assumptions)
• Goals
• Solution paths that are taken into account to produce a solution

The activity should foster self-reflection in order to get students to think about their thinking (metacognition). Therefore, the activity should involve group work that requires (these might be different roles for the group members.):

• Planning
• Monitoring
• Assessing progress

The teams' products should reveal:

• Statistical objects or constructs that were used
• Relationships among the objects and constructs
• Operations or interactions among the objects and constructs
• Representational systems used

The products should allow the instructor or researcher to assess a team's statistical thinking. One method is to create a "Ways of Thinking" chart that categorizes the students' solutions.

5. Model Share-Ability and Reusability Principle: This ensures that solutions created by students are generalizable or easily adapted to other similar situations. The model should represent a general way of thinking instead of a specific solution for a specific context. This principle also ensures that students' models are communicated in a clear understandable manner that allows them to be used by others.

6. Effective Prototype Principle: This ensures that the model produced will be as simple as possible, yet still mathematically significant. The model, which should represent "big ideas" in statistical thinking, should provide a useful learning prototype or metaphor for interpreting other problems with the same underlying structure. The activity should be designed to avoid the need for numerous procedures, especially computational procedures that can circumvent conceptual understanding.