Guiding Students through Sine, Cosine, and Tangent
An Instructor's Guide to Trigonometry in the Geosciences

by Dr. Eric M. Baer, Highline Community College Geology, and Dr. Jennifer M. Wenner, University of Wisconsin, Oshkosh Geology

Jump down to: Difficulties for Students | What's left out? | Resources

What Should the Student Get out of This Module?

When the student finishes this module he or she should be able to:

• calculate the tangent, sine, or cosine of any angle using a calculator
• determine whether an angle is given in degrees or radians and change a calculator's settings to degrees
• calculate any angle in a right triangle, given any two sides
• solve for the length of a side of a right triangle, given an angle and the length of another side
• use inverse trigonometric functions

Why Is It Hard for Students?

We have found that students have difficulty with right-angle trigonometry for a variety of reasons.

• Many students don't have a trigonometric background, or they have not seen it in a long time and so do not remember the formulas for sine, cosine, and tangent (SOH-CAH-TOA). This module provides a refresher for those students.
• A common problem is that students cannot identify when an angle is measured in radians, or they use their calculator in radian mode when they should be using it in degree mode. This is compounded by the fact that they typically use radians in their math classes.
• Students sometimes have difficulty using their calculators correctly when making trigonometry calculations.
• A critical tool is the inverse trig functions like arctangent and arcsine; however few students walk into our classes with experience with inverse functions.
• Finally, students do not have an intuitive idea of the values of sine, cosine, and tangent for most angles and therefore have difficulty recognizing when their answers are wildly wrong. While we don't address this specifically, experience will help.

What Have We Left Out?

This page only deals with solving the most rudimentary of trigonometry problems. It only deals with right triangles and does not use the Law of Sines or the Law of Cosines. We generally have not seen these other applications used in introductory geoscience classes, although their use in the geosciences is abundant.

The page does not help students resolve non-right triangle trig problems into right angle trig problems. We have not typically had students have problems with this as long as they recognize when they are not dealing with a right triangle!

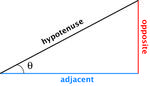
We also do not derive or explore much of the mathematics behind the trigonometric expression or delve into the nature of inverse functions. While these are important, we believe it would be distracting and counterproductive to our goal of having students be able to use these mathematics tools for the purpose of understanding geology. We hope, once they have used these tools in a variety of settings and seen their usefulness, students will have the motivation to explore the underlying mathematics to a greater extent.

Instructor Resources

The Trigonometry and Angles page in the Teaching Quantitative Literacy in the Geosciences website is a terrific place to look for ideas on teaching these topics to introductory geoscience students as well as activities you can use in the classroom and lab.

Angle of Repose is an in-class activity where students make piles from a variety of sediments and measure (either with a protractor or using basic trigonometry) the angle. They examine sediments with different sizes as well as different angularities.

In How Far is Yonder Mountain?—A Trig Problem from Spreadsheets Across the Curriculum, students work through Polya's problem-solving heuristic to find the distance of a peak using vertical angles sighted from a wagon train heading directly for the peak.

Vectors and slope stability is a homework or in-class activity designed for students with little or no experience with vectors or free-body diagrams to apply vectors and trigonometry to slope stability problems. This activity is used in an introductory geohazards course with no prerequisites. It can be completed in one to two hours.

In the first part of Modeling the Interior of the Earth Using Seismic Waves, students use trig to calculate the time of travel for seismic waves through a homogeneous planet.

In An Assessment of Hillslope Stability Using the Factor of Safety, students consider the balance of forces on a hillslope using the Factor of Safety by calculating shear stress and shear strength for an example hillslope and formulating an expression for the factor of safety in an Excel spreadsheet.