Initial Publication Date: July 19, 2011 | Revision: September 19, 2024 (see revision history: 2 events)

Trigonometry Practice Problems

Try solving these as much as you can on your own, and if you need help, look at the hidden solutions. You may use a calculator. You can download a copy of all these questions (Acrobat (PDF) 108kB Jul25 09) to use as you try these on your own.

If you are having difficulty, try the Basic Trig Functions: Practice Problems page.

Calculating the Length of a Side

Length of a path up a hill

You are walking up a 500-meter-high hill. The trail has an incline of 12 degrees. How far will you walk to get to the top?

Show solution

The first step is typically to make a sketch. However, this has been done already, so we will go to step 2, and determine which trig function to use.

Show which trig fuction to use

Step 3 is to rearrange the equation so what you know is on one side and what you don't know is on the other, then substitute in the known values.

Show me how to rearrange this

Finally, we will use a calculator to determine the value of the trigonometric function (sine in this case) and solve for the unknown value.

Show me the next step

Depth to a bed of coal

You note that a bed of coal is tilted at 12 degrees and comes to the surface 6 kilometers from your property. How deep will you have to dig to get to the coal bed on your property?

Show solution

It may help to draw a picture of this. Try it yourself and then see if it looks like the one hidden below

Show hidden diagram

Here we have an angle, 12 degrees, and know the adjacent side (6 km), and we want to know the length of the opposite side (O). The formula that will help us is the tangent:

`text{Tan}=\frac{text{Opposite}}{text{Adjacent}}`

Substituting in the appropriate values,

`text{tan(12)}=\frac{text{O}}{6\ km}`

Rearranging to isolate O,

O = tan(12) * 6 km

Using a calculator, the value of tan(12) is 0.213. So

O = 0.213 * 6 km

So the opposite side of the triangle, the depth of the coal bed, is 1.275 km, or 1275 meters.

Calculating radius of the outer core (seismology)

The S wave shadow zone is caused by the outer core not transmitting S waves. It crosses an arc of 105 degrees on Earth (see the diagram on the left). Estimate the radius of the outer core. The radius of the entire Earth is 6370 km.

Show solution

Again, it will be helpful to draw a diagram.

Show the diagram

Here we have a right triangle with one 52.5-degree angle (half of 105 degrees) and a hypotenuse that is 6370 km long. We need to find the adjacent side, which is the approximate radius of the outer core, so we will use the cosine.

`text{Cos}=\frac{text{Adjacent}}{text{Hypotenuse}}`

Substituting in,

`text{cos(52.5)}=\frac{text{A}}{6370\ km}`

Rearranging for A,

A = cos(52.5) * 6370 km
so
A = 3877 km

So the approximate radius of the core is 3877 km.
Note that this is approximate, because of the bending of the seismic waves as they reflect through the mantle. The actual radius is about 3500 km.

Calculating an Angle

Stream gradient

The Colorado River drops from 3200 feet at Lake Mead to 500 feet in elevation at Lee's Ferry, a river distance of 270 miles. What is the gradient in degrees?

Show solution

Here we have two sides of a triangle and need an angle. The river distance is the hypotenuse and the vertical drop is the opposite angle. However, there is a catch. The measurements are not in the same units, and they must be to use our trigonometric formulas. So first, we'll convert the drop to miles (we could have converted the distance to feet; it doesn't matter.)

`2700\ ft\times\frac{1\ mi}{5280\ ft}=0.511\ mi`

(Note: if you need help with this step you can go to the Unit Conversions page)
Now we can use the formula for sine to calculate the angle x

`text{Sin}=\frac{text{Opposite}}{text{Hypotenuse}`

substituting in,

`text{sin(x)}=\frac{0.511\ mi}{270\ mi}`

sin(x)= 0.00189

to solve for x, the angle, take the inverse sine of each

sin^-1(sin(x)) = sin^-1(0.00189)

since sin^-1(sin(x)) = x , our result is

x = 0.11 degrees

So the slope of the Colorado River is 0.11 degrees.

Angle of repose

The angle of repose is the steepest angle at which dry, unconsolidated sediment is stable. You create a conical pile of sand that is as steep as you can make it. The pile is 11 cm high and has a radius of 16 cm. What is the angle of repose of this sand?

Show solution

Looking at the conical pile from the side, there are 2 right triangles put together. The height is the opposite side of the angle of repose and the radius of the pile is the adjacent side. So we have the information to find the tangent of the angle of repose, which we can call x.

Show next step

`text{Tan}=\frac{text{Opposite}}{text{Adjacent}}`

`text{tan(x)}=\frac{11\ cm}{16\ cm}`

tan(x) = .6875

From this we can solve for x, the angle of repose

Show next step

Plate tectonics and the angle of subduction

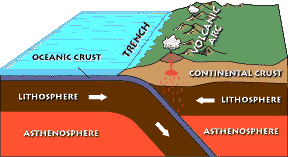Subducting oceanic slabs can plunge steeply or shallowly underneath the overriding plate. In modern subduction zones, the location of earthquakes can show how steeply the subducting slab is plunging into the mantle; however, in ancient subduction zones we cannot use this technique. Instead, we can use the observation that a volcanic arc typically occurs above the point at which the subducting plate reaches a depth of 100 km. If an ancient volcanic arc was 200 km from the trench that marks the initiation of subduction, what is the angle of subduction?

Show solution

In this case one wants to find the angle of where the adjacent side (the distance to the volcanic arc) and the opposite side (the depth of the plate below the volcanic arc) are known, so we will need to use the tangent to find the angle of subduction.

Show next step