Psychic test
 This material was originally developed through
CAUSE
This material was originally developed through
CAUSE as part of its collaboration with the SERC Pedagogic Service.
Summary
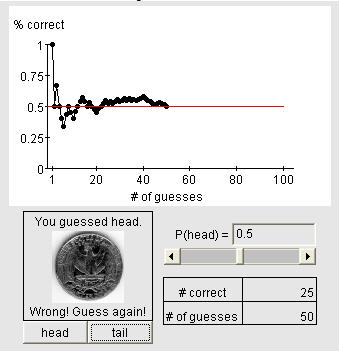
This activity illustrates the convergence of long run relative frequency to the true probability. The psychic ability of a student from the class is studied using an applet. The student is asked to repeatedly guess the outcome of a virtual coin toss. The instructor enters the student's guesses and the applet plots the percentage of correct answers versus the number of attempts. With the applet, many guesses can be entered very quickly. If the student is truly a psychic, the percentage correct will converge to a value above 0.5.
Learning Goals
Context for Use
Teaching Materials
Teaching Notes and Tips
The instructor then introduces the coin tossing applet. The instructor should then return to the original discussion and ask what psychic ability would mean in the context of the applet. The discussion should focus around the idea of P(correctly guessng a toss) > 0.5, the probability associated with an average person randomly guessing the outcome. This value is indicated with a red line in the applet.
The instructor should then ask the class how to use the applet to gauge the student's psychic ability. This will lead to having the student make a large number of guesses in order to estimate the probability of a correct guess. The instructor should have the student make at least 50 guesses with the instructor entering each response for the student by clicking the head and tail buttons. Using the applet allows the guesses to be entered very quickly. Most of the time 50 trials provides a reasonable pattern of convergence.
One can always keep the final percentage/number of guesses and do a formal hypothesis test for psychic ability later in the semester.
Assessment
A quality control engineer believes that the probability of producing a defective item from a manufacturing process is 0.1. Which of the following is true if the engineer's statement is correct?
- The number of defects observed in a large number of sample items produced from the process will converge to 0.1.
- The proportion of defective items in a large number of sample items produced from the process will converge to 0.1.
- The number of defects observed in a large number of sample items produced from the process will converge to 0.5.
- The proportion of defective items in a large number of sample items produced from the process will converge to 0.5.
- 1 out of 10 items produced from the process will be defective.



