Stress and Strain

Initial Publication Date: October 10, 2007

Quantitative concepts: trigonometry, graphing

Stress and Strain

by Dr. Carol Ormand (University of Wisconsin - Madison) and Dr. Eric Baer (Highline Community College)
Jump down to: Stress, strain, & structures | Conditions of deformation | Faults | Analogs | Teaching Examples | Resources

Essential Concepts

There are 5 main concepts with which students struggle when thinking about stress and strain:

  1. rocks deform,
  2. stress causes strain and strain results in structures,
  3. different physical conditions create different structures,
  4. inferring stress from faults, and
  5. the relationship between analogs and reality.

Rocks deform

Many students have a difficult time realizing that rocks can bend or break. They also may have difficulty imagining the forces necessary to fold or fault rocks or comprehending that the seemingly constant Earth can change dramatically over time. This is especially true of students who live in tectonically stable areas. If students are to understand the basics of stress and strain, they must overcome this barrier since it will be difficult to examine the causes and conditions of deformation if students cannot comprehend deformation. It is often helpful to have students create analog models of the structures present in rock photos or hand samples.

Here is a picture of a structure known as boudinage (named after the French word for blood sausage - note the sausage-like structure). Can you make a similar structure using your Silly Putty®?
What kind of rate of strain is necessary to produce something similar (do you get the same result if you pull it apart quickly or more slowly)? Does it work better if your Silly Putty® is warm or cold? Do you think the same result would happen with PlayDoh® or cookie dough? Does the amount of Silly Putty® affect how easily you can reproduce the structure? All of these conditions can be translated to rocks - rate at which it is strained, temperature, type of material, scale - and affect the types of structures that show up in the rock record.

In order to show students that rocks deform, pictures and hand samples of real faulted and folded rocks at a variety of scales can be used. There are several good collections of these types of images such as the AGI Earthscience World Image Bank, Martin Miller's collection, or the National Geophysical Data Center Faults slide set.

Stress causes strain, strain results in structures

Many geologists consider it important for introductory students to understand that visible structures are a record of the stress and physical conditions in the Earth. As a result, the differences between stress, strain and structures formed during strain become key concepts.


After showing pictures of deformed rocks, giving students the opportunity to create their own "structures" with Play-Doh®, Silly Putty® or other geological analog material helps them to understand concepts that underlie stress and strain and allows them to investigate relationships among stress, strain and deformational structures. Students can experiment with types of stress and rates of strain necessary to make analogs break or bend. Alternatively, they can use structures in the analog to infer stresses and strain rates after the "structure" is created. See Rocks deformabove for an example of having students create boudins.

Stress, strain and structure start with the same three letters, yet mean very different things. These words are also used differently in geology than in common usage in English, which can cause confusion. However, here are some tricks that I use to remember:
  • Stress is the same as pressure. When you are under pressure, you are stressed!
  • Stress can happen with out strain, but strain cannot happen without stress.

Look at this rock I am squeezing in my hand.

  • Is it stressed? (Yes, it is under pressure.)
  • Is it strained? (No, it hasn't changed shape.)

Now look at this rock with a fold in it.

  • Is it under stress? (No, it is not under pressure).
  • Is it straining? (No, it isn't currently changing shape.)
  • Does it have structure? (Yes, there is a fold.)

In addition to Silly Putty® and Play-Doh®, wooden blocks with layers drawn in or a compression/squeeze tank filled with layered sand or breakfast cereals also model structural features well. Analogs, however, are difficult to scale appropriately (both in time and space) to the gigantic scale on which geologic structures form. Students may still have difficulty understanding the tremendous scale of forces needed to bend or break rock and the long time scales involved to generate structures. Make sure that you make it clear to your students that these pitfalls exist. More detailed ideas for analogs are available at Teaching Structural Geology analog materials web page.

Once students have mastered the connections among stress, strain and structure, I develop a 3 x 2 table of different structures that form under differing stress and strain conditions. I then proceed to fill out the table with students' help.

Let's look at what features are found under different stress conditions and with different styles of strain. We'll do this by making a table. What are the three types of stress? Compression, tension, and shearing. Now, what are the 2 types of permanent deformation? Ductile and brittle. Let's make a table that is three columns by two rows and fill it in with appropriate structures! When we are finished, we should have 6 kinds of deformation features.

A table of stress and strain and the deformational structures

Now, see if you can make each of those with your Play-Doh® or blocks.

Different conditions lead to different deformation styles

There are many factors that contribute to the style of the deformation in a rock, including pressure, temperature, rock composition, presence or absence of fluids, type of stress, rate of stress, and others. However, the type of stress, the rate of stress and the temperature may be the most critical factors for most introductory students.

silly putty Silly Putty® is a material, just like rocks, that can deform either plastically or brittlely. What controls how it will deform?

  • Temperature: Cold Silly Putty is easy to break, but warm Silly Putty is very plastic.
  • Strain rate: If I pull it apart quickly it breaks, but if I pull it slowly, it stretches (deforms plastically).
  • Type of stress: Finally, pick a strong student, and have him or her try to break the silly putty using compressive stress. As you can see, this is almost impossible. Now have a student try to break it using tension. This is much easier. Most materials are more easily broken (or otherwise deformed) in tension than in compression; we say that they are weaker in tension, or stronger in compression.
Temperature, strain rate, and type of stress are also key factors in deformation within glaciers. This provides a an opportunity to revisit these concepts later in the term.

Relating faults to stress - hanging walls, footwalls, and different types of faults

One of the goals of structural geology is to relate the nature of deformation to the stress that caused it. Therefore, it is important that students be able to distinguish between normal faults (generated by tension) and reverse faults (generated by compression).

Wooden blocks are a valuable tool for teaching about normal and reverse faults. Using three blocks cut on an angle, horsts and grabens can be generated. Pull the blocks apart to create a graben; push them together to make a horst. The advantage of using 3 blocks is that students can see that it is not the orientation of the fault that matters, but the movement on the fault. Because they can see whether I am extending or compressing the blocks, they develop an intuitive sense of the difference between normal and reverse faults. However, students typically still need to learn the difference between the hanging wall and footwall of a fault to be able to accurately determine whether a fault is normal or reverse and what kind of stress caused it.

Faults are places where rocks have been broken and offset. It is not uncommon for fluids to have flowed along the break during deformation, leaving valuable minerals along the fault. As a result, many mines are constructed along fault surfaces. Because of this, one side of the fault is called the hanging wall (the surface from which a miner's lantern would be hung) and one side is called the footwall (the surface on which the miner would walk.)

Showing footwalls and hanging walls

Here's another way to think of it: the hanging wall block is always above the fault plane, while the foot wall block is always below the fault plane. 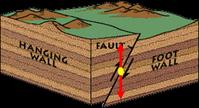Headwall and footwall To see this, put a point on the fault and draw a vertical arrow pointing up. This arrow points into the hanging wall. An arrow pointing straight down points into the footwall. Take a look at the slide that shows the fault and arrows indicating movement. Some students think the footwall looks like a foot. See how the hanging wall is resting, or hanging, on the footwall?

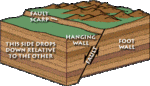normal fault Once students understand the difference between a hanging wall and a footwall, most of them have little trouble remembering that in a reverse fault the hanging wall moves up, indicating compression, and in a normal fault the hanging wall moves down, indicating extension.

As your students can see from these block models, horizontal forces can cause rocks to move along faults that are at an angle to the rock layering. Given that idea, your students can use some basic trigonometric functions to examine the relationship between horizontal strain (the amount of stretching or shortening in a horizontal direction) and displacement on a fault surface (the amount of movement on the fault itself). Since this relationship is dependent on the angle of the fault from horizontal, the angle of the fault is a critical component of how faults accommodate shortening or extension.

Diagram of Seattle Fault Models
The Seattle fault is a large reverse fault that cuts across and underneath the Seattle, Washington, metropolitan area and its nearly 2 million residents. The Seattle fault accommodates about 1 millimeter of shortening per year. However, because the fault plane itself is not well exposed and or discernable in seismic profiles, we don't know what angle this fault makes to horizontal. If the fault is low-angle, at about 25 degrees from horizontal, then to accommodate the 1 mm of shortening it must move 1.1 mm/yr on average. If, however, it is at a more steep 60 degrees, it would need to move 2 mm/yr on average. Since the displacement on the fault is a primary factor in determining the magnitude of an earthquake (see earthquake page), the Seattle fault would need to move either twice as often or have much larger quakes if it is at a steep angle.

Relating analogs to the real Earth

Torn cheese
We often use analogies and analog materials (Silly Putty, sand, wooden blocks, etc.) to illustrate the concepts of stress, strain and the deformation of rocks. However, students sometimes have difficulty relating these materials and their behaviors to the Earth and real rocks. For these students, it may be useful to discuss the rates and magnitudes of deformation in the Earth and the differences between rocks and analog materials. For instance, the rocks at plate boundaries often experience a few centimeters of deformation in a year, but the forces on them are enough to move continents. The size and slowness of these processes are an important concept to communicate, even if they are on a scale that is almost impossible to comprehend. I sometimes tell students that their fingernails are growing at about the same rate the plates are moving, to help them overcome this difficulty.

Plates move at about the same rate as your fingernails grow, a few centimeters per year. While this seems slow, over long periods of time it really adds up. For instance, if you would let your fingernails grow for 100 million years, they would be around 4000 kilometers long!

Teaching Examples

  • Joints in a Cornstarch Analog
    • Desiccated cornstarch-water mixture provides an interactive introduction to joints and joint sets. Students interpret relative ages, examine intersection angles, use surface textures to determine propagation direction, and evaluate the role of flaws in joint initiation.
  • Fracture Fundamentals: A Cheesy Analog
    • This activity has students make small cuts (fracture nuclei) in processed cheese food and then apply stresses perpendicular or parallel to the cuts to see how fractures grow. Surprisingly (or not, depending on one's previous thoughts on cheese), processed cheese food fractures in much the same way as homogeneous rocks.
  • Evolution of Normal Fault Systems During Progressive Deformation
    • This activity is based on QuickTime movies and color digital photographs derived from sandbox experiments that produce normal faults in a variety of boundary conditions following experiments developed by Ken McClay. Students view specially edited movies to gain awareness of the evolution of normal fault systems. They then investigate the formation and evolution of a fault system for a particular structural setting by tracing and labeling individual faults on a set of photographs taken at regular intervals during an experiment. This activity helps students develop an awareness of fault initiation, propagation, rotation, and inactivation during progressive deformation.
  • Analysis of Sidewalk Fractures
    • Using fractures in sidewalks as an analog for natural outcrops, students learn to make systematic observations, measure the orientation and location of fractures, manipulate and analyze data, and consider some kinematic and dynamic questions regarding the origin and significance of fractures.

Resources

  • Teaching Structural Geology in the 21st century
    • This site contains a variety of resources for faculty members who teach undergraduate structural geology. You will find links to activities and assignments, internet and computer resources, useful articles and maps, presentations from the summer 2004 workshop on teaching structural geology, working groups and a discussion forum, and lots of creative ideas for teaching structural geology.
  • 3D visualizations of structural deformation (more info)
    • GeoBlocks 3D, created by Steve Reynolds, contains interactive QuickTime Virtual Reality (QTVR) movies exploring the three-dimensional nature of geology, specifically geologic structures within blocks. You can rotate the blocks, make them partially transparent to view their internal structure, cut through or erode them, displace faults, and more.
  • Structural Geology of Rocks and Regions (introductory chapter)
    • This textbook by Davis and Reynolds is the most widely used structural geology text according to a recent survey. The introductory chapter may be helpful for faculty in thinking about how to teach this section of an intro class since it examines the three basic ways structural geologists examine deformation: geometric analysis, kinematic analysis and dynamic analysis.
  • Steve Reynolds' web page (more info)
    • This page contains many visualization tools and other resources, developed and gathered by Steve Reynolds, geology professor at Arizona State University.
  • Structural Geology Course Resources on the Internet
    • A catalog of courses with on-line resources or web-pages