Teaching quantitative concepts in floods and flooding
Quantitative concepts: probability,recurrence intervals, rates
by Dr. Eric M. Baer, Geology Program, Highline Community College
Jump down to: Rating Curves | Inundation | Flood forecasts | Resources and activities
Essential Concepts
Generally there are five main concepts that our students struggle with when thinking about floods:

- the various ways that we measure the size or flow of a river,
- the relationship between discharge and stage,
- how a rise in flood stage leads to an area of inundation,
- flood forecasts, probabilities, recurrence intervals and how to calculate them,
- the meaning of a "100-year flood".
Discharge, stage, flood stage, and crest: What's the difference?
Students often get confused by the variety of ways the size or magnitude of flows in rivers are measured and communicated. It is not that these concepts are difficult, however if these terms are not explicitly defined, students often end up perplexed.
- Discharge is the volume of water that passes through a given cross section per unit time, usually measured in cubic feet per second (cfs) or cubic meters per second (cms).
- Stage is the level of the water surface over a datum (often sea level). As discharge increases, stage increases, however the relationship is not linear.
- Flood stage is the stage at which overbank flows are of sufficient magnitude to cause considerable inundation of land and roads and/or significantly threaten life and property. Students often confuse this with overbank flow which is when water overtops the channel and has geomorphic impacts.
- Crest (or peak) is the highest stage reached during a hydrologic event (such as a flood).
In class, and for most hydrologic needs, the discharge (also called flow) is the critical measure of the river. However, it is difficult to measure discharge, so the most common way flows are reported in the media is by stage. In the case of a flood, news reports will often say that a river is "5 feet above flood stage". Floods and rivers also have a crest which is often reported in relationship to flood stage as in "the river will crest at 7 feet above flood stagetomorrow."
Rating a river: the relationship between discharge and stage
The relationship between discharge and stage is empirical and typically is represented graphically as a rating curve.
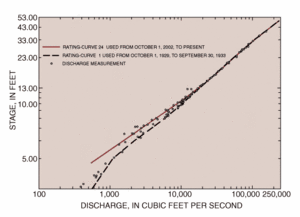
Rating curves are an excellent topic for class discussion because they often seem simple to students at first glance, but are much more complicated. I often ask things like "what happens to a river when the discharge increases?" and then have students explore the rather complicated answers. For example, rating curves may change with time and there is often significant scatter in the data, which can be used as a launching point for discussing regressions and error.
Flood stage and inundation area: it's not just how high the river is
Often students have a difficult time realizing that the area of inundation for a flood depends not just on the stage, but also on the slope of the ground around the water. This is often expressed as students:

- wanting the flood to spread a fixed distance from the stream, independent of topographic changes
- viewing floods as primarily a lateral movement of water rather than a vertical change in the water level (they sometimes think they will get pushed perpendicular to the flow instead of downstream)
These same misconceptions are also true for non-stream flooding events such as tsunami and storm surges where they expect coastal damage to be a fixed distance inland.
To help with these misunderstandings, instead of going straight to a mapping of flood inundation levels on a map,

For some students that really have a hard time visualizing inundation area as a function of topography, I have an inexpensive model of a stream made from a plastic food storage container and modeling clay. I have one stream channel narrow and steep sided and the other broad and relatively flat. I then pour water into the model to simulate the rise of water from a flood and see the difference in inundation area. In the steep valley they can see that the flood does not spread far away from its original channel whereas in the broader valley the area under water is much greater.
Flood forecasting: forecasts based on historic data and the "100-year flood"

The determination of recurrence intervals has many inherent assumptions that are often false. One assumption is that each flood event is independent of previous flooding events, which is often false. Another assumption is that the occurrences and recurrence intervals of floods in the past is the same as the occurrences in the future. Because drainage basins are changed by human activities and other events, and rainfall may be changing due to local or global climate variations, the extrapolation of past events to the future may be invalid.
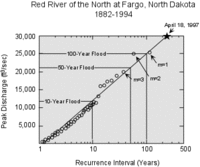
The extrapolations of recurrence intervals are then to forecast the future probability of a flood of a given discharge. The probability (P) of an flood with recurrence interval T is
P = 1/T
So a flood discharge that has a 100-year recurrence interval has a 1% chance of occurring or being exceeded in a given year. The stage of such a flood can be back-calculated using the rating curve for the river. Once the stage is known, a topographic map can be consulted to examine inundation.
An example of taking historical discharges to forecasted inundations
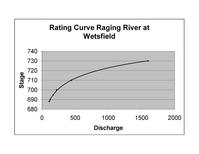
They first gather data from a local stream gauge which shows the maximum annual stage each year. Unfortunately, the gauge has only been operating for 16 years. They then assign a recurrence interval to each of the year's peak floods.
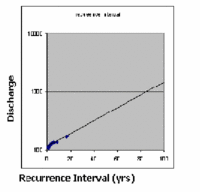
What is a one hundred year flood?
The term "a one-hundred year flood" is actually a misnomer, and as a result causes a great deal of confusion with students and professionals alike. What is really meant by this term is a flood with recurrence interval of 100 years - one that has a 1% chance of occurring in any given year. There are several ideas and resources for teaching recurrence intervals for floods and other events on the recurrence interval page.
Teaching resources and activities
- Flood Frequency and Risk Assessment
- Rethinking Flood Prediction: Why the Traditional Approach Needs to Change
Student Resources
- Information from FEMA about flood hazards and mitigation (more info)
- Floods and floodplains (U.S. Geological Survey Open File Report 93-641) contains general background information on floods.
- Significant Floods in the United States During the 20th Century - USGS Measures a Century of Floods ( This site may be offline. ) lists thirty-two of the most significant floods (in terms of number of lives lost and (or) property damage) in the United States during the 20th century according to the various types of floods. Internet sites for acquiring near-real-time streamflow data and other pertinent flood information are provided.
- The "1OO-Year Flood" explains how and when uncommon big floods happen.
- You can view up-to-date information on national flood-threat forecast from the National Weather Service and NOAA.
- Water resources in the United States from the U.S.G.S. ( This site may be offline. ) This is an entry site into many resources including water data regional studies and more.
- Water resources data from the U.S.G.S. (more info) This page provide access to water-resources data collected at more than 1 million sites in all 50 States, the District of Columbia, and Puerto Rico.
