X-ray reflection in accordance with Bragg's Law
When a crystal is bombarded with X-rays of a fixed wavelength (similar to spacing of the atomic-scale crystal lattice planes) and at certain incident angles, intense reflected X-rays are produced when the wavelengths of the scattered X-rays interfere constructively. In order for the waves to interfere constructively, the differences in the travel path must be equal to integer multiples of the wavelength. When this constructive interference occurs, a diffracted beam of X-rays will leave the crystal at an angle equal to that of the incident beam.
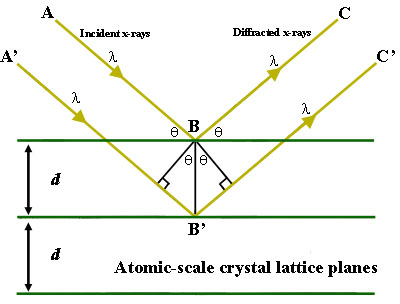
To illustrate this feature, consider a crystal with crystal lattice planar distances d (right). Where the travel path length difference between the ray paths ABC and A'B'C' is an integer multiple of the wavelength, constructive interference will occur for a combination of that specific wavelength, crystal lattice planar spacing and angle of incidence (Θ). Each rational plane of atoms in a crystal will undergo refraction at a single, unique angle (for X-rays of a fixed wavelength).
The general relationship between the wavelength of the incident X-rays, angle of incidence and spacing between the crystal lattice planes of atoms is known as Bragg's Law, expressed as:
n λ = 2d sinΘ
where n (an integer) is the "order" of reflection, λ is the wavelength of the incident X-rays, d is the interplanar spacing of the crystal and Θ is the angle of incidence.
Applications of Bragg's Law.
- In X-ray diffraction (XRD) the interplanar spacing (d-spacing) of a crystal is used for identification and characterization purposes. In this case, the wavelength of the incident X-ray is known and measurement is made of the incident angle (Θ) at which constructive interference occurs. Solving Bragg's Equation gives the d-spacing between the crystal lattice planes of atoms that produce the constructive interference. A given unknown crystal is expected to have many rational planes of atoms in its structure; therefore, the collection of "reflections" of all the planes can be used to uniquely identify an unknown crystal. In general, crystals with high symmetry (e.g. isometric system) tend to have relatively few atomic planes, whereas crystals with low symmetry (in the triclinic or monoclinic systems) tend to have a large number of possible atomic planes in their structures.
- In the case of wavelength dispersive spectrometry (WDS) or X-ray fluorescence spectroscopy (XRF), crystals of known d-spacings are used as analyzing crystals in the spectrometer. Because the position of the sample and the detector is fixed in these applications, the angular position of the reflecting crystal is changed in accordance with Bragg's Law so that a particular wavelength of interest can be directed to a detector for quantitative analysis. Every element in the Periodic Table has a discrete energy difference between the orbital "shells" (e.g. K, L, M), such that every element will produce X-rays of a fixed wavelength. Therefore, by using a spectrometer crystal (with fixed d-spacing of the crystal) and positioning the crystal at a unique and fixed angle (Θ), it is possible to detect and quantify elements of interest based on the characteristic X-ray wavelengths produced by each element.
Literature
Eby, G.N., 2004, Principles of Environmental Geochemistry. Brooks/Cole-Thomson Learning, p. 212-214.
Related Resources
Bragg's Law Applet Activity, Glenn Richard
This teaching activity provides an introduction to Bragg's Law and has students use a Java applet to explore and answer questions. The activity was developed for the On the Cutting Edge, Understanding the Deep Earth workshop.
