How Do I Change Units on a Number?
Unit Conversions in the Geosciences
Unit conversions can also be called:
Dimensional analysis
Unit analysis
Factor label method
Introduction to Unit Conversions
Geologic map of the San Andreas Fault system from the
USGS In the geosciences, we think about how Earth works on a variety of scales. For example, the San Andreas Fault that runs nearly the length of California's coastline is more than 1200 km long. But we talk about movement on the fault in terms of mm per year. So, we have to be able to think about thousands of km and a few mm when talking about the same feature. In addition, a geoscientist who lives in the United States needs to be able to think in terms of English and metric units, because the public thinks in terms of English units (miles, gallons, etc.) and the scientific community uses SI units (kilometers, liters, etc.). This may seem difficult at first, but it is crucial for anyone studying geosciences to be able to move easily from one unit to another (with a little calculation, of course). Luckily, there are some simple steps that, if followed, can help you complete unit conversions with relative ease.
Photo of conversion of speed limit signs near the US–Canada border.
How Do I Do a Unit Conversion?
You can do any unit conversion if you follow a few simple steps. Although there is no single "right" way to do unit conversions, these steps provide one way to learn to do unit conversions. DO NOT SKIP ANY STEPS! Although it may seem tedious, working through unit conversions requires that each of these steps be followed so that you can be sure that you end up with what you want, especially when you are just starting out with learning to do unit conversions.
Below, you can download and print some tables for your use when doing unit conversions:
- If you are converting from one metric unit to another, this list of metric prefixes (Acrobat (PDF) 7kB Aug31 11) will be useful.
- When converting from metric to imperial (sometimes called English) units (or vice versa), this conversion chart (Acrobat (PDF) 40kB Sep3 09) might be helpful.
When you do any unit conversion, you should always know what units you started with and what units you want to end up with. This is key to success at unit conversions.
The Steps
The steps to successfully completing a unit conversion are outlined below. To illustrate the steps, let's use a geologic example: In Southern California, slip on the San Andreas Fault is on the order of 25 km/Myr. How many cm does the San Andreas Fault move in one year?
- Write (copy) out the units that you are given as a fraction.
In this case, you are given km/Myr.
`\frac{25\text{km}}{1\text{Myr}}`
OR you could write that you have kilometers (km is a length or distance) and Myr (which is Megayears or million years, a period of time).
- Write out the units that you want at the end of the conversion as a fraction:
In the example, you are asked to convert km/Myr to cm/year, so you want to end up with cm/year.
`\frac{text{cm}}{text{yr}}`
OR you could write that you want your units to have centimeters (cm; a length or distance) and years (yr; a time).
- Determine appropriate conversion factors. Use tables in your textbook or download one of the tables listed above (for this particular example, you probably only need to know the prefixes for metric system (Acrobat (PDF) 7kB Aug31 11)).
For our example of movement on the San Andreas Fault, we need to convert 1 km to cm and Myr (Mega-years or Million years) to years, so with the handy guide to metric system prefixes, we need three conversion factors:
- 1 km = 1,000 m
- 1 m = 100 cm
- 1 Myr = 1,000,000 yr
- Evaluate the appropriate arrangement for conversion factors. That is, copy the conversion factor(s) from step 3 into fraction form so that the units end up canceling. Remember that when you multiply fractions (as you will in step 6 below), you can cancel units ONLY when they appear in the numerator of one fraction and the denominator of another.
We're going to have to do several steps in this conversion and we have to start somewhere. Let's start with converting km/year to cm/year. Because km is on top, we're going to want to arrange the conversion fraction so that km is in the bottom position (denominator) like so:
`\frac{1000text{m}}{1text{km}}`
or you could start setting up your conversion:
`\frac{25\text{km}}{1\text{Myr}} \times \frac{1000text{m}}{1text{km}}`
Now we can cancel km
`\frac{25}{1\text{Myr}} \times \frac{1000text{m}}{1}`
but even when we cancel km, we're still left with m in the numerator so we need another conversion that has m in the denominator like this:
`\frac{100text{cm}}{1text{m}}`
We can add our next conversion factor to the string of fractions we're going to eventually multiply:
`\frac{25\text{km}}{1\text{Myr}} \times \frac{1000text{m}}{1text{km}} \times \frac{100text{cm}}{1text{m}}`
and we can cancel appropriate units:
`\frac{25}{1\text{Myr}} \times \frac{1000}{1} \times \frac{100text{cm}}{1}`
Now we have what we want in the numerator, but we still have Myr in the denominator. So, we need a conversion factor that has Myr in the numerator:
`\frac{1text{Myr}}{1","000","000text{yr}}`
Add another fraction to the string:
`\frac{25\text{km}}{1\text{Myr}} \times \frac{1000text{m}}{1text{km}} \times \frac{100text{cm}}{1text{m}} \times \frac{1text{Myr}}{1","000","000text{yr}}`
and then cancel units:
`\frac{25}{1} \times \frac{1000}{1} \times \frac{100text{cm}}{1} \times \frac{1}{1","000","000text{yr}}`
- Set up the conversion by writing the fractions in a row with multiplication signs in between.
(You may have already done this if you set the conversion up as you wrote out the conversion factors.)
`\frac{25\text{km}}{1\text{Myr}} \times \frac{1000text{m}}{1text{km}} \times \frac{100text{cm}}{1text{m}} \times \frac{1text{Myr}}{1","000","000text{yr}}`
- Evaluate. Do the original units cancel so that you end up with what the question is asking for? If not, repeat steps 2 and 3 until they do!
`\frac{25}{1} \times \frac{1000}{1} \times \frac{100text{cm}}{1} \times \frac{1}{1,000,000text{yr}}`
(like units are canceled with the same color in the example above) Note that the only units that are not canceled are cm (in the numerator) and yr (in the denominator) so the units on your answer will be cm/yr!
- Now, let's do some arithmetic: To complete the conversion, we multiply all the numerators and then all the denominators (or multiply across the top and bottom).
`\frac{25}{1} \times \frac{1000}{1} \times \frac{100text{cm}}{1} \times \frac{1}{1","000","000text{yr}}=\frac{2","500","000text{cm}}{1","000","000text{yr}}`
If you are unsure about how I got the numbers here, you can review what is meant by "multiply across top and bottom" below:
When fractions are multiplied, you need to keep track of numbers on the top (also called the numerator) and bottom (also called the denominator).
- It's easier to keep track of these numbers if you write the fractions like this: `\frac{25\text{km}}{1\text{Myr}}`. In this case, the numerator is 25 km and the denominator is 1 Myr.
- To multiply fractions, treat top and bottom numbers separately (multiply top numbers and then multiply bottom numbers).
`\frac{25}{1} \times \frac{1000}{1} \times \frac{100text{cm}}{1} \times \frac{1}{1","000","000text{yr}}=\frac{25 \times 1000 \times 100 text{cm} \times 1}{1 \times 1 \times 1 \times 1","000","000text{yr}}`
- Write out your new numbers as a fraction (the top product as the numerator; the bottom product as the denominator)
`\frac{25}{1} \times \frac{1000}{1} \times \frac{100text{cm}}{1} \times \frac{1}{1","000","000text{yr}}=\frac{25 \times 1000 \times 100 text{cm} \times 1}{1 \times 1 \times 1 \times 1","000","000text{yr}}=\frac{2","500","000text{cm}}{1","000","000text{yr}}`
- Reduce the fraction by dividing numerator by denominator once you have the top and bottom multiplied.
`\frac{25}{1} \times \frac{1000}{1} \times \frac{100text{cm}}{1} \times \frac{1}{1","000","000text{yr}}=\frac{2","500","000text{cm}}{1","000","000text{yr}}=\frac{2.5text{cm}}{text{yr}}`
This can also be written as 2.5 cm/yr (said "centimeters per year").
- EVALUATE (again). Is this a reasonable number?
Considering that plate motions are in the range of 1–10 cm/yr, 2.5 cm/yr is a reasonable answer!
You can download and print a sheet with the unit conversion steps (Acrobat (PDF) 44kB Apr11 08)to use while completing the practice problems.
Just a quick note about the metric system: Although the United States is one of the last holdouts on the imperial or English system of measurement (inches, miles,
°F, etc.), the metric system is often much more intuitive because it is a system of base 10 numbers. The nice thing about dividing numbers in the metric system is that when you get to the end, you can actually cancel out the zeros in the fraction (remember, you have to cancel the same number on the top and bottom; there may be a few left over in either the numerator or the denominator). For example, in the question above:
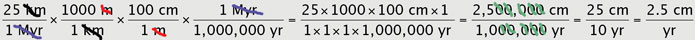
so that you only have to divide 25 by 10. If you are rusty about what the prefixes mean for the metric system, you can review the order of magnitude for a "femtogram" or "gigabyte" or any other SI unit using the
metric prefixes (Acrobat (PDF) 7kB Aug31 11) document available earlier on the page.
Where Are Unit Conversions Used in the Geosciences?
- Plate tectonics: converting rates of plate motion, etc.
- Topographic maps: converting scales
- Rivers and streams: converting rates of flow, slope, etc.
- Groundwater: converting rates of flow
- Glaciers: converting rates of flow (or retreat), etc.
- Geologic time: converting time, rates of deposition, etc.
And many other topics . . .
Next Steps
I am ready to PRACTICE!
If you think you have a handle on the steps above, click on this bar to try practice problems with worked answers.
Or, if you want even more practice, see 'More help' below.
More Help with Unit Conversions
Some tables of conversion factors
Help with unit conversions (dimensional analysis)
Help with multiplying fractions
This page was written and compiled by Dr. Jennifer M. Wenner, Geology Department, University of Wisconsin, Oshkosh, and Dr. Eric M. Baer, Geology Program, Highline Community College





