Single-crystal X-ray Diffraction
Christine M. Clark, Eastern Michigan University
Barbara L. Dutrow, Louisiana State University
What is Single-crystal X-ray Diffraction
Single-crystal X-ray Diffraction is a non-destructive analytical technique which provides detailed information about the internal lattice of crystalline substances, including unit cell dimensions, bond-lengths, bond-angles, and details of site-ordering. Directly related is single-crystal refinement, where the data generated from the X-ray analysis is interpreted and refined to obtain the crystal structure.
Fundamental Principles of Single-crystal X-ray Diffraction
Max von Laue, in 1912, discovered that crystalline substances act as three-dimensional diffraction gratings for X-ray wavelengths similar to the spacing of planes in a crystal lattice. X-ray diffraction is now a common technique for the study of crystal structures and atomic spacing.
X-ray diffraction is based on constructive interference of monochromatic X-rays and a crystalline sample. These X-rays are generated by a cathode ray tube, filtered to produce monochromatic radiation, collimated to concentrate, and directed toward the sample. The interaction of the incident rays with the sample produces constructive interference (and a diffracted ray) when conditions satisfy Bragg's Law (nλ=2d sinθ). This law relates the wavelength of electromagnetic radiation to the diffraction angle and the lattice spacing in a crystalline sample. These diffracted X-rays are then detected, processed and counted. By changing the geometry of the incident rays, the orientation of the centered crystal and the detector, all possible diffraction directions of the lattice should be attained.
All diffraction methods are based on generation of X-rays in an X-ray tube. These X-rays are directed at the sample, and the diffracted rays are collected. A key component of all diffraction is the angle between the incident and diffracted rays. Powder and single-crystal diffraction vary in instrumentation beyond this.
Interpretation of data:
Typical mineral structures contain several thousand unique reflections, whose spatial arrangement is referred to as a diffraction pattern. Indices (hkl) may be assigned to each reflection, indicating its position within the diffraction pattern. This pattern has a reciprocal Fourier transform relationship to the crystalline lattice and the unit cell in real space. This step is referred to as the solution of the crystal structure. After the structure is solved, it is further refined using least-squares techniques. This procedure is described fully on the single-crystal structure refinement (SREF) page.
Single-crystal X-ray Diffraction Instrumentation - How Does It Work?
X-ray diffractometers consist of three basic elements, an X-ray tube, a sample holder, and an X-ray detector. X-rays are generated in a cathode ray tube by heating a filament to produce electrons, accelerating the electrons toward a target by applying a voltage, and impact of the electrons with the target material. When electrons have sufficient energy to dislodge inner shell electrons of the target material, characteristic X-ray spectra are produced. These spectra consist of several components, the most common being Kα and Kβ. Kα consists, in part, of Kα1 and Kα2. Kα1 has a slightly shorter wavelength and twice the intensity as Kα2. The specific wavelengths are characteristic of the target material. Filtering, by foils or crystal monochrometers, is required to produce monochromatic X-rays needed for diffraction. Kα1and Kα2 are sufficiently close in wavelength such that a weighted average of the two is used. Molybdenum is the most common target material for single-crystal diffraction, with MoKα radiation = 0.7107Å. These X-rays are collimated and directed onto the sample. When the geometry of the incident X-rays impinging the sample satisfies the Bragg Equation, constructive interference occurs. A detector records and processes this X-ray signal and converts the signal to a count rate which is then output to a device such as a printer or computer monitor. X-rays may also be produced using a synchotron, which emits a much stronger beam.
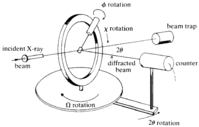
Single-crystal diffractometers use either 3- or 4-circle goniometers. These circles refer to the four angles (2θ, χ, φ, and Ω) that define the relationship between the crystal lattice, the incident ray and detector. Samples are mounted on thin glass fibers which are attached to brass pins and mounted onto goniometer heads. Adjustment of the X, Y and Z orthogonal directions allows centering of the crystal within the X-ray beam.
X-rays leave the collimator and are directed at the crystal. Rays are either transmitted through the crystal, reflected off the surface, or diffracted by the crystal lattice. A beam stop is located directly opposite the collimator to block transmitted rays and prevent burn-out of the detector. Reflected rays are not picked up by the detector due to the angles involved. Diffracted rays at the correct orientation for the configuration are then collected by the detector.
Modern single-crystal diffractometers use CCD (charge-coupled device) technology to transform the X-ray photons into an electrical signal which are then sent to a computer for processing.
Applications
Single-crystal X-ray diffraction is most commonly used for precise determination of a unit cell, including cell dimensions and positions of atoms within the lattice. Bond-lengths and angles are directly related to the atomic positions. The crystal structure of a mineral is a characteristic property that is the basis for understanding many of the properties of each mineral. Specific applications of single-crystal diffraction include:
- New mineral identification, crystal solution and refinement
- Determination of unit cell, bond-lengths, bond-angles and site-ordering
- Characterization of cation-anion coordination
- Variations in crystal lattice with chemistry
- With specialized chambers, structures of high pressure and/or temperature phases can be determined
- Determination of crystal-chemical vs. environmental control on mineral chemistry
- Powder patterns can also be derived from single-crystals by use of specialized cameras (Gandolfi)
Strengths and Limitations of Single-crystal X-ray Diffraction?
Strengths
- No separate standards required
- Non-destructive
- Detailed crystal structure, including unit cell dimensions, bond-lengths, bond-angles and site-ordering information
- Determination of crystal-chemical controls on mineral chemistry
- With specialized chambers, structures of high pressure and/or temperature phases can be determined
- Powder patterns can also be derived from single-crystals by use of specialized cameras (Gandolfi)
Limitations
- Must have a single, robust (stable) sample, generally between 50—250 microns in size
- Optically clear sample
- Twinned samples can be handled with difficulty
- Data collection generally requires between 24 and 72 hours
User's Guide - Sample Collection and Preparation
Sample Selection and Preparation
Samples for single-crystal diffraction should be selected from unfractured, optically clear crystals. This can be determined by viewing the samples under crossed polars on a petrographic microscope. Crystals can be broken off a larger sample and the best fragment selected. Samples should be between 30 and 300 microns, with ideal crystals averaging 150-250 microns in size. To minimize absorption affects, equant crystals are preferred. Spherical crystals can be created using a small, air-powered crystal tumbler, however easily cleaved minerals can break during this process. Therefore, minerals lacking cleavage are the best choice for this step. If the sample is inequant, this must be corrected for during absorption corrections to the data.
Samples are mounted on the tip of a thin glass fiber using an epoxy or cement. Care should be taken to use just enough epoxy to secure the sample without embedding it in the mounting compound. The fiber may be ground to a point to minimize absorption by the glass. This fiber is attached to a brass mounting pin, usually by the use of modeling clay, and the pin is then inserted into the goniometer head.
Sample Centering
The goniometer head and sample are then affixed to the diffractometer. Samples can be centered by viewing the sample under an attached microscope or video camera and adjusting the X,Y and Z directions until the sample is centered under the cross-hairs for all crystal orientations.
Data Collection, Results and Presentation
Data Collection
Once the crystal is centered, a preliminary rotational image is often collected to screen the sample quality and to select parameters for later steps. An automatic collection routine can then be used to collect a preliminary set of frames for determination of the unit cell. Reflections from these frames are auto-indexed to select the reduced primitive cell and calculate the orientation matrix (which relates the unit cell to the actual crystal position within the beam). The primitive unit cell is refined using least-squares and then converted to the appropriate crystal system and Bravias lattice. This new cell is also refined using least-squares to determine the final orientation matrix for the sample.
After the refined cell and orientation matrix have been determined, intensity data is collected. Generally this is done by collecting a sphere or hemisphere of data using an incremental scan method, collecting frames in 0.1° to 0.3° increments (over certain angles while others are held constant). For highly symmetric materials, collection can be constrained symmetrically to reduce the collection time. Data is typically collected between 4° and 60° 2θ for molybdenum radiation. A complete data collection may require anywhere between 6-24 hours, depending on the specimen and the diffractometer. Exposure times of 10-30 seconds per frame for a hemisphere of data will require total run times of 6-13 hours. Older diffractometers with non-CCD detectors may require 4-5 days for a complete collection run.
Corrections for Background, Absorption, etc.
After the data have been collected, corrections for instrumental factors, polarization effects, X-ray absorption and (potentially) crystal decomposition must be applied to the entire data set. This integration process also reduces the raw frame data to a smaller set of individual integrated intensities. These correction and processing procedures are typically part of the software package which controls and runs the data collection.
Phase Problem and Fourier Transformation
Once the data have been collected, the phase problem must be solved to find the unique set of phases that can be combined with the structure factors to determine the electron density and, therefore, the crystal structure. A number of different procedures exist for solution of the phase problem, but the most common method currently, due to the prevalence of high-speed computers, is using direct methods and least-squares, initially assigning phases to strong reflections and iterating to produce a refined fit.
Structure solution
Solution of the phase problem leads to the initial electron density map. Elements can be assigned to intensity centers, with heavier elements associated with higher intensities. Distances and angles between intensity centers can also be used for atom assignment based on likely coordination. If the sample is of a known material, a template may be used for the initial solution. More information about structure solution and refinement can be found on the single-crystal structure refinement page.
Structure Refinement
Once the initial crystal structure is solved, various steps can be done to attain the best possible fit between the observed and calculated crystal structure. The final structure solution will be presented with an R value, which gives the percent variation between the calculated and observed structures. The single-crystal structure refinement page provides further information on the processes and steps involved in refining a crystal structure.
Literature
The following literature can be used to further explore Single-crystal X-ray Diffraction
- Campana, C.F., Bruker Analytical Application Note
- Putnis, A. (1992). Introduction to Mineral Sciences. Cambridge, UK: Cambridge University Press. Chapter 3 (pp. 41-80).
Related Links
For more information about Single-crystal X-ray Diffraction follow the links below.
- An Introduction to the Scope, Potential and Applications of X-ray Analysis, from the International Union of Crystallography
- American Mineralogist Crystal Structure Database
- International Centre for Diffraction Data
- X-ray Powder Diffraction--USGS Publication
- X-ray Instruments--University of California, Santa Barbara
- Crystallography Clearinghouse--IUCR
- Reciprocal Net--part of the National Science Digital Library. Use the "Learn About" link to find animations of the structures of common molecules (including minerals), crystallography learning resources (tutorials, databases and software), resources on crystallization, and tutorials on symmetry and point groups.
- Crystallography Tutorials -- Sean Parkin, University of Kentucky
Teaching Activities and Resources
Teaching activities, labs, and resources pertaining to Single-crystal X-ray Diffraction.
- Cambridge University X-ray Tutorial
- International Union of Crystallography (IUCr) Teaching Pamphlets
- Introduction to X-ray Diffraction (more info) --University of California, Santa Barbara
- Introduction to Crystallography --from LLNL
- X-ray Crystallography Lecture Notes ( This site may be offline. ) --from Steve Nelson, Tulane University
- Neil E. Johnson, 2001, X-Ray Diffraction Simulation using Laser Pointers and Printers , Journal of Geoscience Education, vol 49 #4, p. 346



![[reuse info]](/images/information_16.png)





