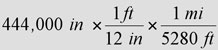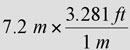- First Publication: July 19, 2011
- Revision: September 19, 2024 -- Updated website to improve accessibility of images math equations and chrome.
Unit Conversions Practice Problems
Some Simple Unit Conversion Problems
If you do not have a list of common conversion factors in your book, you may wish to download and print this sheet of common conversion factors for the geosciences (Acrobat (PDF) 40kB Sep3 09). Open the link below to use while you make your calculations.
If you need a reminder of the steps, you can download and print this worksheet (Acrobat (PDF) 44kB Apr11 08) walking you through the steps for unit conversion.
Finally, you can download a sheet that has all the problems (Acrobat (PDF) 48kB Jul25 09) on it so you can print it out and work them on your own.
If you need a reminder of the steps, you can download and print this worksheet (Acrobat (PDF) 44kB Apr11 08) walking you through the steps for unit conversion.
Finally, you can download a sheet that has all the problems (Acrobat (PDF) 48kB Jul25 09) on it so you can print it out and work them on your own.
Rate Problems
Show credits
HideA photo of a speed limit sign on Long Road in Cambridge, UK. From the October/November 2006 newsletter of the Cambridge Cycling Campaign.
- 120 km/hr
Let's do this using the steps you learned in the previous page.
- Write out the units you have (when appropriate as a fraction):
`\frac{120text{km}}{1text{hr}}` - Write out the units you want to end with:
`\frac{?text{mi}}{1text{hr}}` - Determine appropriate conversion factors (in some cases, there will be more than one conversion factor for each of the units you have):
Since "hours" stays the same on the bottom, you only need one conversion factor: km to mi. So, you can write 1km = 0.6214 mi - Evaluate the appropriate arrangement for fractions (that is, what units belong in the numerator (top) of fraction? What units need to be in the denominator (bottom)? Remember, units cancel when one unit is in the numerator and the other is in the denominator). Remember that when you multiply fractions (as you will in step 6 below), you can cancel units ONLY when they appear in both the numerator and the denominator.
Since km is in the numerator in the original units, km needs to be in the denominator so that we can cancel:
`\frac{0.6214text{mi}}{1text{km}}` - Set up the conversion by writing the fractions in a row with multiplication signs in between:
`\frac{120text{km}}{1text{hr}} \times \frac{0.6214text{mi}}{1text{km}}`
- Evaluate. Do the original units cancel so that you are left with ONLY the units asked for? If not, repeat steps 3 and 4 until you are left with the appropriate units:
We cancel km and end with mi/hr (which is what we want!)
`\frac{120}{1text{hr}} \times \frac{0.6214text{mi}}{1}` - Multiply across top and bottom:
`\frac{120}{1text{hr}} \times \frac{0.6214text{mi}}{1} = \frac{74.6text{mi}}{1text{hr}}` - If necessary, reduce the fraction.
`\frac{120}{1text{hr}} \times \frac{0.6214text{mi}}{1} = 74.6 frac{text{mi}}{text{hr}}`
- Evaluate your answer.
Is a speed limit of about 75 mph (mi/hr) a reasonable speed limit? If you got 0.75 or 75,000, would you recognize that it is not reasonable?
- 75 km/hr
- Write out the units you have (when appropriate as a fraction):
`\frac{75text{km}}{1text{hr}}` - Write out the units you want to end with:
`\frac{?text{mi}}{1text{hr}}` - Determine appropriate conversion factors (in some cases, there will be more than one conversion factor for each of the units you have):
Since "hours" stays the same on the bottom, you only need one conversion factor: km to mi. So, you can write 1km = 0.6214 mi - Evaluate the appropriate arrangement for fractions (that is, what units belong in the numerator (top) of fraction? What units need to be in the denominator (bottom)? Remember, units cancel when one unit is in the numerator and the other is in the denominator). Remember that when you multiply fractions (as you will in step 6 below), you can cancel units ONLY when they appear in both the numerator and the denominator.
Since km is in the numerator in the original units, km needs to be in the denominator so that we can cancel:
`\frac{0.6214text{mi}}{1text{km}}` - Set up the conversion by writing the fractions in a row with multiplication signs in between:
`\frac{75text{km}}{1text{hr}} \times \frac{0.6214text{mi}}{1text{km}}`
- Evaluate. Do the original units cancel so that you are left with ONLY the units asked for? If not, repeat steps 3 and 4 until you are left with the appropriate units:
We cancel km and end with mi/hr (which is what we want!)
`\frac{75}{1text{hr}} \times \frac{0.6214text{mi}}{1}` - Multiply across top and bottom:
`\frac{75}{1text{hr}} \times \frac{0.6214text{mi}}{1} = \frac{46.6text{mi}}{1text{hr}}` - If necessary, reduce the fraction.
`\frac{75}{1text{hr}} \times \frac{0.6214text{mi}}{1} = 46.6 frac{text{mi}}{text{hr}}`
- Evaluate your answer.
Is a speed limit of about 46 mph (mi/hr) a reasonable speed limit? If you got 120 or 0.075, would you recognize that it is not reasonable?
- 50 km/hr
- Write out the units you have (when appropriate as a fraction):
`\frac{50text{km}}{1text{hr}}` - Determine appropriate conversion factors (in some cases, there will be more than one conversion factor for each of the units you have):
Since "hours" stays the same on the bottom, you only need one conversion factor: km to mi. So, you can write 1 km = 0.6214 mi - Evaluate the appropriate arrangement for fractions (that is, what units belong in the numerator (top) of fraction? What units need to be in the denominator (bottom)? Remember, units cancel when one unit is in the numerator and the other is in the denominator). Remember that when you multiply fractions (as you will in step 6 below), you can cancel units ONLY when they appear in both the numerator and the denominator.
Since km is in the numerator in the original units, km needs to be in the denominator so that we can cancel:
`\frac{0.6214text{mi}}{1text{km}}` - Set up the conversion by writing the fractions in a row with multiplication signs in between:
`\frac{50text{km}}{1text{hr}} \times \frac{0.6214text{mi}}{1text{km}}`
- Evaluate. Do the original units cancel so that you are left with ONLY the units asked for? If not, repeat steps 3 and 4 until you are left with the appropriate units:
We cancel km and end with mi/hr (which is what we want!)
`\frac{50}{1text{hr}} \times \frac{0.6214text{mi}}{1}` - Multiply across top and bottom:
`\frac{50}{1text{hr}} \times \frac{0.6214text{mi}}{1} = \frac{31.1text{mi}}{1text{hr}}` - If necessary, reduce the fraction.
`\frac{50}{1text{hr}} \times \frac{0.6214text{mi}}{1} = 31.1 frac{text{mi}}{text{hr}}`
- Evaluate your answer.
Is a speed limit of about 30 mph (mi/hr) a reasonable speed limit? If you got 0.80 mph or 30,000 mph, would you recognize that it is not reasonable?
Density Conversions (Multiple-Step Problems)
Problem 2: Geologists' observations suggest that the two most common rocks exposed at the surface of Earth are granite (continental crust) and basalt (oceanic crust). From travel times of earthquake waves, we also know that the average density of Earth is about 5.5 g/cm3. See if you can do some unit conversions using information given in the questions below to determine whether the whole Earth could be made of these two rock types only.
- As an astute observer walking around on continental crust (granite), you might decide to test the hypothesis that the Earth is made entirely of granite. You weigh a 1.00 cubic ft piece of granite on your home scale and find that it weighs 171 lbs. Thus, you determine that the granite has a density of 171 lb/ft3. Convert your granite's density to g/cm3. Given the information above, could the earth be made completely of granite?
Let's go through this using the steps from the Unit Conversions Page.
- Copy the number and units as a fraction:
`\frac{171\ lb}{1\ ft^{3}}`
Because the block of granite is 1 cubic foot, you can put 1 on the bottom of the fraction. - Write out the units you want to end with:
`\frac{g}{cm^{3}}` - Look up the conversion factors for what you have (pounds and feet (or cubic feet)) to what you want (grams and cm (or cubic cm)).
pounds to grams:
1 lb = 453.3924 g
feet to cm:
1 foot = 30.48 cm
feet to cubic feet:
1 ft * 1 ft * 1 ft = 1 ft3
cubic feet to cubic centimeters:
1 ft3 = 30.48 cm * 30.48 cm * 30.48 cm = 28,316 cm3
- Take note of what you have and what you want to end up with. Then, write out conversion factors from step 2 as fractions so that units cancel.
You want to be able to cancel lb (so that unit has to be on the bottom of the converting fraction) and ft3 (so that unit has to be on the top of the converting fraction):
`\frac{171\ lb}{1\ ft^{3}}\times\frac{453.5924\ g}{1\ lb}\times\frac{1\ ft^{3}}{28316\ cm^{3}}` - Once you have written all the conversion fractions so that the original value is being multiplied by them (see last step), evaluate. Do the original units cancel so that you end up with what the question is asking for?
`\frac{171}{1}\times\frac{453.5924\ g}{1}\times\frac{1}{28316\ cm^{3}}`
- Multiply the fractions (across the top and bottom):
`\frac{171}{1}\times\frac{453.5924\ g}{1}\times\frac{1}{28316\ cm^{3}}=\frac{77564\ g}{28316\ cm^{3}}`
- Divide the resulting number to get an answer.
`\frac{171}{1}\times\frac{453.5924\ g}{1}\times\frac{1}{28316\ cm^{3}}=\frac{77564\ g}{28316\ cm^{3}}=2.74\frac{g}{cm^{3}}`
- Is this a reasonable answer?
This isn't the answer we were looking for: 5.5 g/cm3. But it is within an order of magnitude. It is also a number that is greater than the density of water (which is 1 g/cm3) and we know that granite is denser than water! So it's a reasonable number. However, it shows that Earth cannot be made completely of granite!
- Given that basalt seems to well up when ocean crust pulls apart at Mid-Ocean ridges, you might decide that maybe the entire Earth is made of basalt. On your bathroom scale, a 64 in3 (4 in x 4 in x 4 in) block of basalt weighs 116 ounces. Use this information to calculate whether the average density of Earth (5.5 g/cm3) can be explained by an Earth made completely of basalt.
Let's go through this using the steps from the Unit Conversions Page.- Copy the number and units as a fraction:
`\frac{116\ oz}{64\ text{in}^{3}}`
- Write out the units you want to end with:
`\frac{g}{cm^{3}}` - Look up the conversion factors for what you have (pounds and feet [or cubic feet]) to what you want (grams and cm [or cubic cm]).
oz to grams:
1 oz = 28.349523 g
in to cm:
1 inch = 2.54 cm
inches to cubic inches:
1 in * 1 in * 1 in = 1 in3
cubic in to cubic centimeters:
1 in3 = 2.54 cm * 2.54 cm * 2.54 cm = 16.4 cm3
- Take note of what you have and what you want to end up with. Then, write out conversion factors from step 2 as fractions so that units cancel.
You want to be able to cancel oz (so that unit has to be on the bottom of the converting fraction) and in3 (so that unit has to be on the top of the converting fraction): `\frac{116\ oz}{64\ text{in}^{3}}\times \frac{28.349523\ g}{1\ oz}\ \times\frac{1\ text{in}^{3}}{16.4\ cm^{3}}`
- Once you have written all the conversion fractions so that the original value is being multiplied by them (see last step), evaluate. Do the original units cancel so that you end up with what the question is asking for?
`\frac{116}{64}\times\frac{28.349523\ g}{1}\ \times\frac{1}{16.4\ cm^{3}}`
- Multiply the fractions (across the top and bottom):
`\frac{116}{64}\times\frac{28.349523\ g}{1}\ \times\frac{1}{16.4\ cm^{3}}=\frac{3288.5\ g}{1049.6\ cm^{3}}`
- Divide the resulting number to get an answer.
`\frac{116}{64}\times\frac{28.349523\ g}{1}\ \times\frac{1}{16.4\ cm^{3}}=\frac{3288.5\ g}{1049.6\ cm^{3}}=3.13\ \frac{g}{cm^{3}}`
- Is this a reasonable answer?
This isn't the answer we were looking for: 5.5 g/cm3. But it is within an order of magnitude. It is also a number that is greater than the density of water (which is 1 g/cm3) and we know that basalt is denser than water (it sinks)! So it's a reasonable number. However, it shows that Earth cannot be made completely of basalt either! So, there must be something denser down there—like the iron/nickel core!
Scaling Problems
Three maps showing three different scales. From the USGS Rocky Mountain Mapping Center activity Teaching about ScaleProblem 3: You are working with a map that has a fractional scale of 1:24,000 (meaning that 1 unit on the map is equal to 24,000 units on the ground: 1 mm = 24,000 mm or 1 in = 24,000 in). See if you can determine solutions to the following problems that geologists face when working with maps.
- You are hiking to a field area and measure the length of the trail as 18.5 inches. Calculate how many miles you have to hike to get to the interesting rocks/geology?
This is actually a two-step conversion problem. First you have to convert your map measurements to measurements on the ground. Then you can convert to units that you understand.First, think about what you have (18.5 in on the map and a scale) and what you want to know (how many miles 18.5 inches represents on the ground). It may help to think about inches on the map and inches on the ground as different units.
To begin, write the fractional scale as a fraction (with the distance on the ground on top, since that is what we want to ultimately end up with).
`18.5\ text{in on the map}\times\frac{24","000\ text{in on the ground}}{1\ text{in on the map}}=444","000\ text{in on the ground}`
You have just calculated how many inches you have to cover on the trail. But that just seems like a lot, so let's convert those inches to miles!
First, let's write out the appropriate conversion factors:
1 foot = 12 inches
and
1 mile = 5280 feet.
Next, we have to write these conversion factors as fractions. Remember to arrange them so that units you don't want to cancel, and you end up with units that you do want!
`444","000\ text{in}\times\frac{1\ ft}{12\ text{in}}\times\frac{1\ mi}{5280\ ft}`
Then we can cancel units. Do we end up with miles?
`444","000\times\frac{1}{12}\times\frac{1\ mi}{5280}`
Yes! Now we multiply across the top and bottom (note that the bottom number doesn't have any units because both are canceled by others):
`444","000\ text{in}\times\frac{1\ ft}{12\ text{in}}\times\frac{1\ mi}{5280\ ft}=\frac{444","000\ mi}{63,360}\ `
And when we clear fractions:
`444","000\ text{in}\times\frac{1\ ft}{12\ text{in}}\times\frac{1\ mi}{5280\ ft}=7.0\ mi`
We find that our hike will be 7 miles! - Once you get to your field area, you are going to create a geologic map of that area. You have a mechanical pencil that has a lead that is 0.3 mm thick. The smallest feature you can map will be something that is 0.3 mm wide on the map. How wide (in m) can that feature be?
This, like problem 3.1 is actually a two-step conversion problem. First you have to convert your map measurements to measurements on the ground. Then you can convert to units that you understand.First, think about what you know (0.3 mm on the map and a scale) and what you want to know (how many meters 0.3 mm represents on the ground). It may help to think about mm on the map and mm on the ground as different units.
To begin, write the fractional scale as a fraction (with the distance on the ground on top (since that is what we want ultimately to end up with)).
`0.3\ mm\ text{on the map}\times\frac{24,000\ mm\ text{on the ground}}{1\ mmtext{on the map}}=7,200\ mm\ text{on the ground}`
You have just calculated how many millimeters thick a feature can be. But, because this is the metric system, we can modify that so that you don't have to keep a lot of zeros in your head.
First, let's write out the appropriate conversion factors:
1 m = 1000 mm
Next, we have to write these conversion factors as fractions. Remember to arrange them so that units you don't want cancel, and you end up with units that you do want!
`7200\ mm\times\frac{1\ m}{1000\ mm}`
Finally, cancel the appropriate units (mm in this case) and multiply across the top and bottom.
`7200\times\frac{1\ m}{1000}=\frac{7200\ m}{1000}=7.2\ m`
You can map any feature wider than 7.2 m.
The cool thing about the metric system is that it is based in the number 10. This means that conversions within the metric system involve moving zeros around. It also means that when doing calculations, many times you can cancel out zeros.
How does this work? Zeros can only be canceled if they occur on the top and bottom of a fraction. In the problem above, you can cancel two zeros on either side of the fraction:
`7200\times\frac{1\ m}{1000}=\frac{72\ m}{10}=7.2\ m`
Note that the calculation then becomes 72 divided by 10. Most of us can easily divide by 10, making this calculation much easier. In fact, when you get to that point, you may not even need a calculator. Keep this in mind as you do calculations! - Now you have an idea of the size of features that can be drawn on your map. Convert your answer in problem 3.2 to feet.
This is a simple conversion with only one step.The conversion factor listed in the table (see link above) is
1 m = 3.281 feet. First let's set up our equation with fractions:
`7.2\ m\times\frac{3281\ ft}{1\ m}`
Then cancel units and multiply top and bottom
`7.2\ m\times\frac{3281\ ft}{1\ m}=\frac{23.6\ ft}{1}=23.6\ ft`
You can map a feature that is about 24 feet wide.
Next Steps
TAKE THE QUIZ!!
I think I'm competent with unit conversions and I am ready to take the quiz! This link takes you to WAMAP. If your instructor has not given you instructions about WAMAP, you may not have to take the quiz.Still Need More Practice?
There are numerous websites that have practice problems for unit conversions. Several of them are listed below. Please use these links for more practice with unit conversions!- Dr. Crystal Yau in the chemistry department at Community College of Baltimore County has a worksheet that you can download called Practice problems on Unit Conversions (Acrobat (PDF) 110kB Oct9 07). The answers are included.
- The Science Spot's Metric Mania Page has two worksheets that have unit conversion practice problems (answers are provided but not worked through):
- Oak Road Systems has several practice problems with answers (but not worked through).
- Scott Van Bramer at Weidner University has a number of links to unit conversion practice problems from length to volume and so on. You can check your answers within the practice web pages.
- Jerry Artz at Hamline College has sample Unit Conversion problems, problem set 1 with some complex unit conversions, and Problem set 2 with word problems. All of these links include answers.
- The School of Technology at Purdue University has three sets of Unit Conversion Practice problems. Answers are provided but not worked through.
- Math Goodies has a worksheet with some word problems having to do with dimensional analysis. Link to answer key in the box below the image of the worksheet.
- Alan's Chemistry page has some quizzes (take Quiz 4 or 5) that deal with dimensional analysis (and significant figures).
- Copy the number and units as a fraction:
- Write out the units you have (when appropriate as a fraction):
