How to read an equation
How to Read an Equation
Points to Keep in Mind
Some key points to keep in mind when discussing interpretation of equations with students:
- Making the connection between a mathematical expression and its physical meaning is a challenging problem for many geoscience students, regardless of discipline. They're not the only ones struggling with this.
- They need to grasp that understanding what the equations mean is the most important point.
- The power of mathematics is that it expresses what we know in a clear, precise and succinct form. Mathematics lets us write down very precisely what we know.
Keeping variables and constants straight
An important point to clarify for students is identification of constants and variables in the equations they're using. This is particularly true in courses in which the students may be less comfortable with mathematical representations. Keep in mind that what may seem obvious to the instructor is not at all obvious to most of your students. For example, let us consider a simple algebraic expression that will be encountered in many courses, namely the Ideal Gas Law. Many students are familiar with this equation in the following form:
pV=nRT
where p is the pressure, V is the volume, T is the temperature, n is the number of moles of the gas in the volume and R is the universal gas constant. Meteorology students will see it in a form adapted for the atmosphere:
Pα=RdT
where α is the volume per unit mass (specific volume or the inverse of the density) and Rd is R divided by the mean molecular weight of dry air. It is the gas constant for dry air.
Using the latter form, P, α, and T are variables and Rd is a constant.
If we pose a question like: "What will happen to the pressure as the air temperature near the ground warms up on a sunny day?" Students will frequently say that the pressure will also go up. They see the p and T as proportional (ignoring the other terms in the equation) and they answer based upon this apparent association. They can then be reminded that pressure in the atmosphere is hydrostatic, that is, it is due to the weight of the air column above. Thus, the pressure will not change as the temperature rises. It is the other variable in the expression, the specific volume of the air parcel, that will increase.
Understanding the physical meaning of the terms in an equation
Similarly, students can be asked why air cools as it rises. Many will again say it is because the pressure goes down as the parcel ascends, again recognizing the apparent proportionality while ignoring again that the volume is variable and that the volume would increase as the parcel ascended. The relative amounts that α and T will change by as p decreases is not determined by the Ideal Gas Law since in this case it is a single equation with two unknowns, α and T.
Therefore, recognizing the difficulties they have in applying algebraic expressions, instructors must be especially cautious in carefully identifying and emphasizing which terms are variables, which are constant, and what are the physical meanings of the variables and the terms in which they appear.
Consider another slightly more complex expression, namely an expression originating in the First Law of Thermodynamics describing the rate of change of temperature as governed by energy conservation principles:
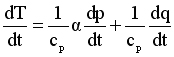
Reading this expression, it says that the rate of change of temperature is the result of the combination of two factors. The first term on the right hand side includes the specific volume and the rate of change of pressure as variables, and the second term includes the diabatic heating rate, which would usually be specified (not a variable).
dT/dt = rate of change of temperature
αdp/dt = specific volume times the rate of change of pressure
dq/dt = rate at which heat is being added or removed from the air parcel
Simple Cases of Interpretation
Simply, then, if the pressure is constant, adding heat to the air will increase the air temperature. In that case:

The proportionality is easy to see.
If the situation is adiabatic, then dq/dt=0. In this case,

This means that the temperature will change only if the pressure changes following the motion of a parcel of air. This can only happen if the air moves up or down, thus reducing or increasing the pressure.
